题目内容

3．某种定点投篮游戏的规则如下：每人投篮10次，如果某同学某次没有投进，则罚该同学做俯卧撑2个．现有一同学参加该游戏，已知该同学在该点投篮的命中率为0.6，设该同学参加本次比赛被罚做俯卧撑的总个数记为X，则X的数学期望为（　　）
A．4B．6C．8D．12

分析 设该同学没有投进的次数为ξ，则ξ～B（10，0.4），利用X=2ξ．EX=2Eξ，即可得出．

解答 解：设该同学没有投进的次数为ξ，则ξ～B（10，0.4），Eξ=10×0.4=4，
则X=2ξ．
∴EX=2Eξ=2×4=8．
故选：C．

点评 本题考查了二项分布列及其数学期望，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
13．若关于x的不等式$|{x-\frac{1}{2}}|+|{x+\frac{3}{2}}|＜k$的解集不是空集，则实数k的取值范围是k＞2．
14．已知数列{an}的前n项和Sn满足4an-3Sn=2，其中n∈N*．则数列{an}的通项公式为an=2•4n-1．
11．已知幂函数f （ x ）过点（2，$\sqrt{2}$），则f （ 9 ）的值为（　　）
A．$\frac{1}{3}$B．1C．3D．6
18．由于电子技术的飞速发展，计算机的成本不断降低，若每隔5年计算机的价格降低$\frac{1}{3}$，问现在价格为5400元的计算机经过15年后，价格应降为1600 元．
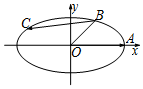8．如图，椭圆的方程为$\frac{x^2}{6}+\frac{y^2}{2}$=1，A是其右顶点，B是该椭圆在第一象限部分上的一点，且∠AOB=$\frac{π}{4}$．若点C是椭圆上的动点，则$\overrightarrow{OA}•\overrightarrow{BC}$的取值范围为[-9，3]．
15．阅读如右图所示的程序框图，则输出的值是（　　）
A．6B．18C．27D．124
12．命题p：?x∈R，函数$f（x）=2{cos^2}x+\sqrt{3}sin2x≤3$的否定为?x0∈R，函数f（x0）=2cos2x0+$\sqrt{3}$sin2x0＞3．
13．已知$a={（\frac{1}{3}）^{\frac{1}{2}}}，b={log_{\frac{1}{2}}}\frac{1}{3}，c={log_3}\frac{1}{2}$则（　　）
A．C＞b＞aB．b＞c＞aC．b＞a＞cD．a＞b＞c

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网