题目内容
16.甲、乙两人进行定点投篮比赛,在距篮筐3米线内设一点A,在点A处投中一球得2分,不中得0分,在距篮筐3米线段外设一点B,在点B处投中一球得3分,不中得0分,已知甲乙两人在A点投中的概率都是$\frac{1}{2}$,在B点投中的概率都是$\frac{1}{3}$,且在A,B两点处投中与否相互独立,设定甲乙两人现在A处各投篮一次,然后在B处各投篮一次,总得分高者获胜.(Ⅰ)求甲投篮总得分ξ的分布列和数学期望;
(Ⅱ)求甲获胜的概率.
分析 (Ⅰ)由已知得ξ的可能取值为0,2,3,5,分别求出相应的概率,由此能求出ξ的分布列和Eξ.
(Ⅱ)由(Ⅰ)得乙投篮总得分X的分布列,由此能求出甲获胜的概率.
解答 解:(Ⅰ)由已知得ξ的可能取值为0,2,3,5,
P(ξ=0)=$\frac{1}{2}×\frac{2}{3}$=$\frac{2}{6}$=$\frac{1}{3}$,
P(ξ=2)=$\frac{1}{2}×\frac{2}{3}$=$\frac{2}{6}$=$\frac{1}{3}$,
P(ξ=3)=$\frac{1}{2}×\frac{1}{3}$=$\frac{1}{6}$,
P(ξ=5)=$\frac{1}{2}×\frac{1}{3}$=$\frac{1}{6}$,
∴ξ的分布列为:
| ξ | 0 | 2 | 3 | 5 |
| P | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{6}$ | $\frac{1}{6}$ |
(Ⅱ)由(Ⅰ)得乙投篮总得分X的分布列为:
| X | 0 | 2 | 3 | 5 |
| P | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{6}$ | $\frac{1}{6}$ |
点评 本题考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意相互独立事件概率乘法公式的合理运用.

练习册系列答案
相关题目
7.已知变量x与y线性相关,且由观测数据算得样本平均数分别为$\overline{x}$=4,$\overline{y}$=3,则由该观测数据算得的线性回归方程不可能是( )
| A. | $\widehat{y}$=0.2x+2.2 | B. | $\widehat{y}$=0.3x+1.8 | C. | $\widehat{y}$=0.4x+1.4 | D. | $\widehat{y}$=0.5x+1.2 |
11.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{5}}}{3}$,椭圆上一点P到两焦点距离之和为12,则b=( )
| A. | 8 | B. | 6 | C. | 5 | D. | 4 |
1.下列函数中,既是偶函数又在区间(0,+∞)上单调递增的是( )
| A. | $y=\frac{1}{x}$ | B. | y=lgx | C. | y=|x|-1 | D. | $y={({\frac{1}{2}})^{lnx}}$ |

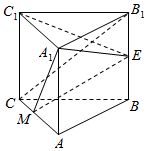 如图.在三棱柱ABC-A1B1C1中,已知侧棱与底面垂直,∠CAB=90°,且AC=1,AB=2,E为BB1的中点,M为AC上一点,$\overrightarrow{AM}$=$\frac{2}{3}$$\overrightarrow{AC}$.
如图.在三棱柱ABC-A1B1C1中,已知侧棱与底面垂直,∠CAB=90°,且AC=1,AB=2,E为BB1的中点,M为AC上一点,$\overrightarrow{AM}$=$\frac{2}{3}$$\overrightarrow{AC}$.