题目内容
函数f（a）=cos2θ+acosθ-a（a∈[1，2]，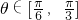
）的最小值是
- A.
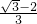
- B.cos2θ+cosθ-1
- C.
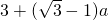
- D.cos2θ+2cosθ-2
D
分析：注意观察，f（a）=cos2θ+acosθ-a，这是关于a的一次函数，利用其单调性即可求其最小值．
解答：∵
，
∴cosθ-1＜0，
∴f（a）=cos2θ+acosθ-a=（cosθ-1）a+cos2θ在[1，2]上单调递减，
∴f（a）的最小值为：f（2）=cos2θ+2cosθ-2．
故选D．
点评：本题考查函数的性质，关键在于把握f（a）=cos2θ+acosθ-a的本质是关于a的一次函数，易错点在于受到cosθ的影响而出错，属于中档题．
分析：注意观察，f（a）=cos2θ+acosθ-a，这是关于a的一次函数，利用其单调性即可求其最小值．
解答：∵
，∴cosθ-1＜0，
∴f（a）=cos2θ+acosθ-a=（cosθ-1）a+cos2θ在[1，2]上单调递减，
∴f（a）的最小值为：f（2）=cos2θ+2cosθ-2．
故选D．
点评：本题考查函数的性质，关键在于把握f（a）=cos2θ+acosθ-a的本质是关于a的一次函数，易错点在于受到cosθ的影响而出错，属于中档题．
练习册系列答案
相关题目
已知函数f（x）=cos（x+?）（0＜?＜π）的导函数f'（x）的图象如图所示，则?=（ ）A、
| ||
B、
| ||
C、
| ||
D、
|