题目内容
过双曲线C:
-
=1(a>0,b>0)的左焦点F的直线l与双曲线C的右支交于点P,与x2+y2=a2恰好切于线段FP的中点M,则直线l的斜率为( )
| x2 |
| a2 |
| y2 |
| b2 |
分析:设双曲线的右焦点为F',由三角形中位线定理可得|PF1|=2|OM|=2a,结合双曲线的定义:|PF|-|PF1|=2a,算出|PF|=4a,最后在Rt△PFF'中利用三角函数的定义,算出∠PFF'的正切值,可得直线l的斜率.
解答:解:设双曲线的右焦点为F',
∵原点O为FF'的中点,线段FP的中点为M,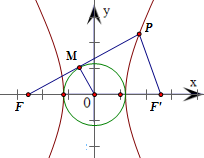
∴OM为△PFF'的中位线,可得|PF'|=2|OM|=2a,
∵由双曲线的定义可知:|PF|-|PF'|=2a,
∴|PF|=|PF'|+2a=4a,
由OM⊥PF,可得PF'⊥PF,
∴Rt△PFF'中,tan∠PFF'=
=
,即直线l的斜率为
.
故选:D
∵原点O为FF'的中点,线段FP的中点为M,

∴OM为△PFF'的中位线,可得|PF'|=2|OM|=2a,
∵由双曲线的定义可知:|PF|-|PF'|=2a,
∴|PF|=|PF'|+2a=4a,
由OM⊥PF,可得PF'⊥PF,
∴Rt△PFF'中,tan∠PFF'=
| |PF′| |
| |PF| |
| 1 |
| 2 |
| 1 |
| 2 |
故选:D
点评:本题给出双曲线
-
=1的一条焦半径与圆x2+y2=a2恰好相切于它的中点,求焦半径所在直线的斜率.着重考查了直线的斜率、双曲线的定义与标准方程和直线与圆的位置关系等知识,属于中档题.
| x2 |
| a2 |
| y2 |
| b2 |

练习册系列答案
相关题目
 过双曲线
过双曲线