Question

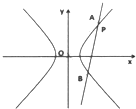过双曲线C：

x2

a2

-

y2

b2

=1上一点P作一直线交双曲线C渐近线于A，B两点，且满足

AP

=λ

PB

，求△AOB的面积．

Answer 1

分析：根据题意设A（am，bm），B（an，-bn），由

AP

=λ

PB

算出点P坐标关于m、n、λ的表达式，代入双曲线方程算出mn=

(1+λ)2

4λ

．利用直线的斜率公式和二倍角的三角函数公式算出sin∠AOB=

2ab

a2+b2

，由两点的距离公式算出OA、OB的长，根据三角函数的面积公式加以计算即可得到△AOB的面积S=

(1+λ)2

4λ

ab．

解答：解：根据题意，可得双曲线的渐近线为y=±

b

a

x，
设A（am，bm），B（an，-bn），m、n均为正数，设P（x₁，y₁）
∵

AP

=λ

PB

，
∴

x1= am+λan 1+λ y1= bm-λbn 1+λ

，可得P（

am+λan

1+λ

，

bm-λbn

1+λ

）
将点P坐标代入双曲线方程，得

( am+λan 1+λ )2

a2

-

( bm-λbn 1+λ )2

b2

=1，
即

(m+λn)2

(1+λ)2

-

(m-λn)2

(1+λ)2

=1，化简得mn=

(1+λ)2

4λ

．
设直线y=

b

a

x的倾斜角为α，则tanα=

b

a

，
∴sin∠AOB=sin2α=

2tanα

1+tan2α

=

2• b a

1+( b a )2

=

2ab

a2+b2

，
∵OA=

(am)2+(bm)2

=m

a2+b2

，OB=

(an)2+(bn)2

=n

a2+b2

，
∴△AOB的面积S=

1

2

OA•OBsin∠AOB=

1

2

mn（a²+b²）

2ab

a2+b2

=

(1+λ)2

4λ

ab．

点评：本题给出双曲线的渐近线上点A、B和双曲线上的点P，在满足

AP

=λ

PB

的情况下求△AOB的面积，着重考查了双曲线的简单几何性质、直线的倾斜角、二倍角的三角函数公式和三角形的面积计算等知识，属于中档题．