题目内容
若函数 是R上的奇函数
是R上的奇函数
(1)求a的值,并利用定义证明函数f(x)在R上单调递增;
(2)解不等式: .
.
解:(1)∵f(x)= 是R上的奇函数,
是R上的奇函数,
∴f(0)=0,解得a=2…2分
∴f(x)= .
.
证明:设x1<x2,则f(x1)-f(x2)= -
- …3分
…3分
= …5分
…5分
∵y=2x是R上的增函数,
∴ -
- <0,而(1+
<0,而(1+ )(1+
)(1+ )>0,
)>0,
∴f(x1)-f(x2)<0,即f(x1)<f(x2),
∴函数f(x)在R上单调递增…7分
(2)由f(-2)+f( )≥0,且f(x)是R上的奇函数可得:f(
)≥0,且f(x)是R上的奇函数可得:f( )≥f(2)…8分
)≥f(2)…8分
又f(x)在R上单调递增,
∴ ≥2…9分
≥2…9分
解得0<x≤8…11分
∴不等式的解集是{x|0<x≤8}…12分
分析:(1)依题意,f(0)=0可求得a,从而可得f(x)的解析式,设x1<x2,作差f(x1)-f(x2),化积判断符号即可结论;
(2)利用f(x)为R上的奇函数,且在R上单调递增,将f(-2)+f( )≥0转化为
)≥0转化为 ≥2,解之即可.
≥2,解之即可.
点评:本题考查函数单调性的证明,考查函数奇偶性与单调性的综合应用,考查分析与推理运算能力,属于难题.
 是R上的奇函数,
是R上的奇函数,∴f(0)=0,解得a=2…2分
∴f(x)=
 .
.证明:设x1<x2,则f(x1)-f(x2)=
 -
- …3分
…3分=
 …5分
…5分∵y=2x是R上的增函数,
∴
 -
- <0,而(1+
<0,而(1+ )(1+
)(1+ )>0,
)>0,∴f(x1)-f(x2)<0,即f(x1)<f(x2),
∴函数f(x)在R上单调递增…7分
(2)由f(-2)+f(
 )≥0,且f(x)是R上的奇函数可得:f(
)≥0,且f(x)是R上的奇函数可得:f( )≥f(2)…8分
)≥f(2)…8分又f(x)在R上单调递增,
∴
 ≥2…9分
≥2…9分解得0<x≤8…11分
∴不等式的解集是{x|0<x≤8}…12分
分析:(1)依题意,f(0)=0可求得a,从而可得f(x)的解析式,设x1<x2,作差f(x1)-f(x2),化积判断符号即可结论;
(2)利用f(x)为R上的奇函数,且在R上单调递增,将f(-2)+f(
 )≥0转化为
)≥0转化为 ≥2,解之即可.
≥2,解之即可.点评:本题考查函数单调性的证明,考查函数奇偶性与单调性的综合应用,考查分析与推理运算能力,属于难题.

练习册系列答案
相关题目
 是R上的奇函数
是R上的奇函数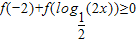 .
. 是R上的奇函数,则
是R上的奇函数,则 ▲ .
▲ .