Question

已知y=f（x）是定义在R上的奇函数，当x≥0时，f（x）=2x-x²．
（1）求y=f（x）的解析式；
（2）画出函数y=f（x）的图象，并指出f（x）的单调区间及在每个区间上的增减性；
（3）若函数y=f（x）的定义域为[a，b]，值域为[

1

b

，  

1

a

] (1≤a＜b)，求实数a、b的值．

Answer 1

分析：（1）由x＜0可得-x＞0，结合x≥0时，f（x）=2x-x²，可求x＜0时的函数解析式，进而可求f（x）
（2）结合函数的图象可判断函数的单调性及单调区间
（3）由f（x）在[1，+∞）上是减函数，且1≤a＜b可得f（x）在[a，b]上是减函数，若函数y=f（x）的定义域为[a，b]，值域为[

1

b

，  

1

a

] (1≤a＜b)，则可得

f(a)= 1 a f(b)= 1 b

，代入可求a，b

解答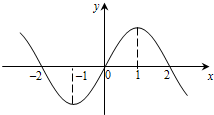：解：（1）当x＜0时，-x＞0，∴f（x）=-f（-x）=-[2（-x）-（-x）²]=2x+x²（2分）
∴f（x）的解析式为  f(x)=

2x-x2 (x≥0) 2x+x2 (x＜0)

（4分）
（2）f（x）的图象如右图：f（x）在（-∞，-1]和[1，+∞）上是减函数f（x）在[-1，1]上是增函数（9分）
（3）∵f（x）在[1，+∞）上是减函数，且1≤a＜b，∴f（x）在[a，b]上是减函数
∴

f(a)= 1 a f(b)= 1 b

（10分）
即 

2a-a2= 1 a 2b-b2= 1 b

（12分）?

(a-1)(a2-a-1)=0 (b-1)(b2-b-1)=0

，
解得 

a=1 或 a= 1± 5 2 b=1 或 b= 1± 5 2

∵1≤a＜b，∴

a=1 b= 1+ 5 2

（13分）

点评：本题主要考查了利用函数的奇偶性求解函数的解析式，由函数的图象判断函数的单调性及单词区间，利用二次函数的单调性求解函数的值域，属于函数知识的综合应用．