题目内容
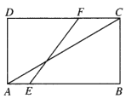
【题目】矩形
中，
，
，点
，
分别是
，
上的动点，将矩形沿
所在的直线进行随意翻折，在翻折过程中直线
与直线
所成角的范围(包含初始状态)为（ ）
A.
B.
C.
D.
【答案】C
【解析】
根据题意，可知初始状态时直线AD与直线BC所成的角为
，当
与
重合时，且当
时，通过勾股定理的逆定理可得
，再利用线面垂直的判定定理和性质可证出
，即可得出在翻折过程中直线
与直线
所成角的范围.
解：由题可知，四边形
是矩形，
，
所以初始状态时直线与直线所成的角为，
已知矩形中，
，
，
则
，
，
由于点
，
分别是
，
上的动点，
当点，分别在
，
处时，即与重合时，
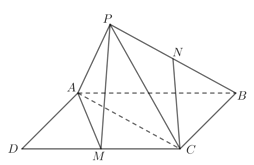
翻折过程中，当时，如下图，
则
，所以，
又
，所以
平面
，
又因为
平面，所以，
此时直线与直线所成的角为
，
所以在翻折过程中直线与直线所成角的范围(包含初始状态)为
.
故选：C.
练习册系列答案
阅读快车系列答案
相关题目
