题目内容
13.在扇形OAB中,∠AOB=105°,C为弧AB上一个动点,若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则x+$\sqrt{2}$y的取值范围是[1,2].分析 可画出图形,然后做CD∥OB,CE∥OA,分别交于OA,OB于D,E,可以说明$x=\frac{|\overrightarrow{OD}|}{|\overrightarrow{OA}|},y=\frac{|\overrightarrow{OE}|}{|\overrightarrow{OB}|}$,而OA,OB都是扇形的半径,从而当C从A运动到B时,$|\overrightarrow{OD}|,|\overrightarrow{OE}|$的变化便反映了x,y的变化,而再由y的系数较大,由图形便可看出C与A重合时,x$+\sqrt{2}y$取到最小值1,而当∠AOC=60°时,$x+\sqrt{2}y$便取到最大值2,这样便得出了x+$\sqrt{2}$y的取值范围.
解答 解:如图,过C作CD∥OB,交OA于D,作CE∥OA,交OB于E,则四边形OECD为平行四边形;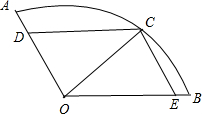
∴$\overrightarrow{OC}=\overrightarrow{OD}+\overrightarrow{OE}$,又$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$;
∴$x\overrightarrow{OA}=\overrightarrow{OD},y\overrightarrow{OB}=\overrightarrow{OE}$;
∴$x=\frac{|\overrightarrow{OD}|}{|\overrightarrow{OA}|},y=\frac{|\overrightarrow{OE}|}{|\overrightarrow{OB}|}$,$|\overrightarrow{OA}|=|\overrightarrow{OB}|$=r;
∴$|\overrightarrow{OD}|,|\overrightarrow{OE}|$的大小反映了x,y的大小;
又y系数较大,当点C沿AB弧由A向B运动的过程中,$|\overrightarrow{OD}|$变短,而$|\overrightarrow{OE}|$变长;
∴由图形可看出:当C和A重合时,x取最大值1,y取最小值0,∴x$+\sqrt{2}y$取到最小值1;
当∠AOC=60°时,x=$\frac{2}{1+\sqrt{3}}$,$y=\frac{2\sqrt{3}}{1+\sqrt{3}}$,∴$x+\sqrt{2}y$取到最大值2;
∴$x+\sqrt{2}y$的取值范围为[1,2].
故答案为:[1,2].
点评 考查向量加法的平行四边形法则,共线向量基本定理,向量数乘的几何意义,结合图形解决问题的方法.

 名校课堂系列答案
名校课堂系列答案| A. | [$\sqrt{3}$-1,$\sqrt{3}$+1] | B. | [$\sqrt{2}-1$,$\sqrt{2}+1$] | C. | [0,2] | D. | [1,2$\sqrt{2}$] |
| A. | x-2y-4=0 | B. | 2x-y-5=0 | ||
| C. | 2x+y-3=0 | D. | 2x-y-5=0或x-2y+4=0 |
| A. | x2>6.635 | B. | x2≤6.635 | C. | x2≤3.841 | D. | x2>3.841 |