题目内容
8.求定积分${∫}_{0}^{4}$($\sqrt{1-(x-1)^{2}}$-x)dx.分析 先根据定积分的几何意义求出${∫}_{0}^{4}$($\sqrt{1-(x-1)^{2}}$=$\frac{π}{2}$,再根据定积分的法则求出${∫}_{0}^{4}$xdx,问题得以解决.
解答 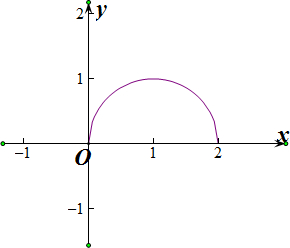 解:${∫}_{0}^{4}$($\sqrt{1-(x-1)^{2}}$-x)dx=${∫}_{0}^{4}$($\sqrt{1-(x-1)^{2}}$dx-${∫}_{0}^{4}$xdx,
解:${∫}_{0}^{4}$($\sqrt{1-(x-1)^{2}}$-x)dx=${∫}_{0}^{4}$($\sqrt{1-(x-1)^{2}}$dx-${∫}_{0}^{4}$xdx,
因为y2=1-(x-1)2表示以(1,0)为圆心,以1为半径的圆,
所以${∫}_{0}^{4}$($\sqrt{1-(x-1)^{2}}$表示以(1,0)为圆心,以1为半径的圆的面积一半,
所以${∫}_{0}^{4}$($\sqrt{1-(x-1)^{2}}$=$\frac{π}{2}$,
所以${∫}_{0}^{4}$($\sqrt{1-(x-1)^{2}}$-x)dx=${∫}_{0}^{4}$($\sqrt{1-(x-1)^{2}}$dx-${∫}_{0}^{4}$xdx=$\frac{π}{2}$-$\frac{1}{2}{x}^{2}$|${\;}_{0}^{4}$=$\frac{π}{2}$-8
点评 本题考查了定积分的几何意义,属于基础题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
4.$\sqrt{{9}^{\frac{3}{2}}}$的值为( )
| A. | $\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 3 | D. | 729 |
16.随着城市车辆的增加,城市的空气污染越来越严重,空气质量指数API一直居高不下,对人体的呼吸系统造成了严重的影响.现调查了某市500名居民的工作场所和呼吸系统健康,得到2×2列联表如下
补全2×2列联表,并回答能否有99%的把握认为“感染呼吸系统疾病和工作场所有关”.
参考公式:x2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$.
| 室外工作 | 室内工作 | 合计 | |
| 有呼吸系统疾病 | 150 | ||
| 无呼吸系统疾病 | 110 | ||
| 合计 | 200 |
| P(Χ2≥k) | 0.050 0.025 0.010 |
| k | 3.841 5.024 6.635 |