题目内容
圆x2+y2+4y=0在点P(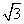 ,-1)处的切线方程为( )
,-1)处的切线方程为( )
A.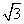 x+y-2=0 B.
x+y-2=0 B.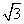 x+y-4=0
x+y-4=0
C.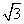 x-y+4=0 D.
x-y+4=0 D.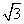 x-y+2=0
x-y+2=0
A
[解析] 解法1:设切线y+1=k(x-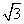 ),
),
即kx-y-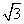 k-1=0.
k-1=0.
则圆心(0,-2)到切线距离等于圆的半径2,
 ,∴k=-
,∴k=-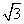 ,
,
∴切线方程为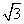 x+y-2=0.
x+y-2=0.
解法2:∵切点A(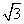 ,-1)与圆心C(0,-2)的连线应与切线垂直.
,-1)与圆心C(0,-2)的连线应与切线垂直.
∴切线斜率k=- =-
=-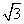 ,
,
∴切线方程为y+1=-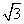 (x-
(x-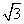 ),即
),即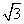 x+y-2=0.
x+y-2=0.
解法3:∵切点A(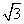 ,-1)在切线上,
,-1)在切线上,
∴排除B、C、D.

练习册系列答案
相关题目
 ,
, ,则角C的大小为( )
,则角C的大小为( ) 在点
在点 处的切线方程为( )
处的切线方程为( ) B.
B. C.
C. D.
D.
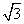 .
.  +
+ =1上,若A点坐标为(3,0),|
=1上,若A点坐标为(3,0),| |=1,且
|=1,且 ·
·