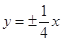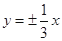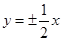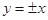题目内容
双曲线 (a>0,b>0)的左右焦点分别为F1,F2,渐近线分别为l1,l2,点P在第一象限内且在l1上,若l2⊥PF1,l2∥PF2,则该双曲线的离心率为( )
(a>0,b>0)的左右焦点分别为F1,F2,渐近线分别为l1,l2,点P在第一象限内且在l1上,若l2⊥PF1,l2∥PF2,则该双曲线的离心率为( )
 (a>0,b>0)的左右焦点分别为F1,F2,渐近线分别为l1,l2,点P在第一象限内且在l1上,若l2⊥PF1,l2∥PF2,则该双曲线的离心率为( )
(a>0,b>0)的左右焦点分别为F1,F2,渐近线分别为l1,l2,点P在第一象限内且在l1上,若l2⊥PF1,l2∥PF2,则该双曲线的离心率为( )A. | B.2 | C.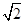 | D.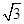 |
B
∵双曲线 (a>0,b>0)的左、右焦点分别为F1,F2,渐近线分别为l1,l2,点P在第一象限内且在l1上,∴F1(-c,0),F2(c,0),P(x,y),渐近线l1的直线方程为y=
(a>0,b>0)的左、右焦点分别为F1,F2,渐近线分别为l1,l2,点P在第一象限内且在l1上,∴F1(-c,0),F2(c,0),P(x,y),渐近线l1的直线方程为y= ,渐近线l2的直线方程为y=-
,渐近线l2的直线方程为y=- ,∵l2∥PF2,∴
,∵l2∥PF2,∴ ,即ay=bc-bx,
,即ay=bc-bx,
∵点P在l1上,即ay=bx,∴bx=bc-bx即x=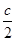 ,∴P(
,∴P(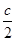 ,
, ),
),
∵l2⊥PF1,∴ ·(-
·(- )=?1,即3a2=b2,因为a2+b2=c2,所以4a2=c2,即c=2a,
)=?1,即3a2=b2,因为a2+b2=c2,所以4a2=c2,即c=2a,
所以离心率e=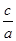 =2.故选B.
=2.故选B.
 (a>0,b>0)的左、右焦点分别为F1,F2,渐近线分别为l1,l2,点P在第一象限内且在l1上,∴F1(-c,0),F2(c,0),P(x,y),渐近线l1的直线方程为y=
(a>0,b>0)的左、右焦点分别为F1,F2,渐近线分别为l1,l2,点P在第一象限内且在l1上,∴F1(-c,0),F2(c,0),P(x,y),渐近线l1的直线方程为y= ,渐近线l2的直线方程为y=-
,渐近线l2的直线方程为y=- ,∵l2∥PF2,∴
,∵l2∥PF2,∴ ,即ay=bc-bx,
,即ay=bc-bx,∵点P在l1上,即ay=bx,∴bx=bc-bx即x=
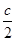 ,∴P(
,∴P(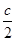 ,
, ),
),∵l2⊥PF1,∴
 ·(-
·(- )=?1,即3a2=b2,因为a2+b2=c2,所以4a2=c2,即c=2a,
)=?1,即3a2=b2,因为a2+b2=c2,所以4a2=c2,即c=2a,所以离心率e=
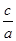 =2.故选B.
=2.故选B.
练习册系列答案
相关题目
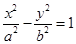 的离心率为
的离心率为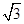 ,则其渐近线方程为( )
,则其渐近线方程为( )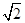 x
x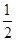 x
x 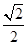 x
x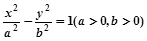 的右焦点为F,若过点F且倾斜角为45°的直线与双曲线的左支没有公共点,则此双曲线离心率的取值范围是( )
的右焦点为F,若过点F且倾斜角为45°的直线与双曲线的左支没有公共点,则此双曲线离心率的取值范围是( )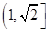

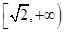
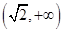
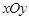 中,若中心在坐标原点的双曲线过点
中,若中心在坐标原点的双曲线过点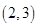 ,且它的一个顶点与抛物线
,且它的一个顶点与抛物线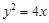 的焦点重合,则该双曲线的方程为 .
的焦点重合,则该双曲线的方程为 . 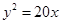 焦点
焦点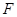 恰好是双曲线
恰好是双曲线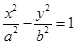 的右焦点,且双曲线过点
的右焦点,且双曲线过点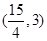 ,则该双曲线的渐近线方程为________.
,则该双曲线的渐近线方程为________.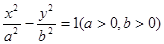 的左、右焦点分别为
的左、右焦点分别为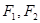 ,若
,若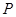 为其上一点,且
为其上一点,且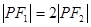 ,
,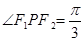 ,则双曲线的离心率为( )
,则双曲线的离心率为( )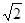
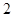
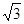
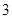
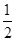 的两条双曲线成为“相近双曲线”。已知双曲线
的两条双曲线成为“相近双曲线”。已知双曲线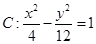 ,则下列双曲线中与
,则下列双曲线中与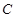 是“相近双曲线”的为( )
是“相近双曲线”的为( )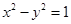

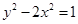
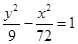
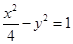 的渐近线方程是
的渐近线方程是
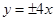
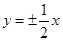
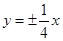
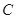 :
: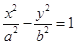 (
(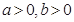 )的离心率为
)的离心率为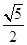 ,则
,则