题目内容
(本题满分12分)
设函数 (a>0,b,cÎR),曲线
(a>0,b,cÎR),曲线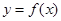 在点P(0,f (0))处的切线方程为
在点P(0,f (0))处的切线方程为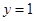 .
.
(Ⅰ)试确定b、c的值;
(Ⅱ)是否存在实数a使得过点(0,2)可作曲线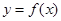 的三条不同切线,若存在,求出a的取值范围;若不存在,请说明理由.
的三条不同切线,若存在,求出a的取值范围;若不存在,请说明理由.
(Ⅰ)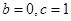 . (Ⅱ)当
. (Ⅱ)当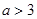 时,过点(0,2)可作曲线
时,过点(0,2)可作曲线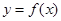 的三条不同切线.
的三条不同切线.
解析试题分析:(Ⅰ)由 得
得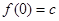 ,
,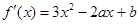
 , ……2分
, ……2分
又由曲线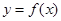 在点P(0,
在点P(0, )处的切线方程为
)处的切线方程为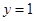 ,得
,得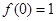 ,
,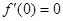 ,故
,故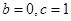 .……4分
.……4分
(Ⅱ)由(Ⅰ)知 ,
,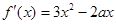 .
.
设存在实数a使得过点(0,2)可作曲线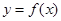 的三条不同切线,并设切点为
的三条不同切线,并设切点为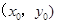 .
.
则切线的斜率为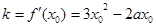 ,
,
切线方程为 ,
, .
.
∵切线过点(0,2),∴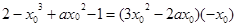 .
.
于是得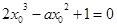 , (*) ……6分
, (*) ……6分
由已知过点(0,2)可作曲线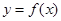 的三条不同切线,则方程(*)应有三个不同实数根.
的三条不同切线,则方程(*)应有三个不同实数根.
令 ,则
,则 .
.
令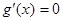 ,得
,得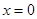 或
或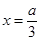 .……8分
.……8分
由于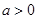 ,所以函数
,所以函数 在区间
在区间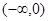 上为增函数,在区间
上为增函数,在区间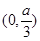 上为减函数,在区间
上为减函数,在区间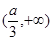 为增函数,所以函数
为增函数,所以函数 在
在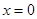 处取极大值
处取极大值 ,在
,在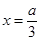 处取极小值
处取极小值 .
.
要使方程(*)有三个不同实数根, ,得
,得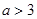 .……11分
.……11分
综上所述,当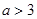 时,过点(0,2)可作曲线
时,过点(0,2)可作曲线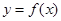 的三条不同切线.……12分
的三条不同切线.……12分
注:如有其它解法,斟情给分.
考点:本题主要考查导数的几何意义,应用导数研究函数的单调性及极值,简单不等式解法。
点评:典型题,本题属于导数应用中的基本问题,(2)作为存在性问题,先假定存在实数a使得过点(0,2)可作曲线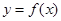 的三条不同切线,通过研究函数的单调性,认识函数特征,转化成只需使方程
的三条不同切线,通过研究函数的单调性,认识函数特征,转化成只需使方程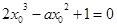 有三个不同实数根,得到a的不等式。
有三个不同实数根,得到a的不等式。

练习册系列答案
相关题目
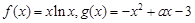 .
.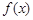 在
在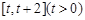 上的最小值;
上的最小值;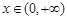 ,
,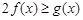 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.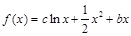
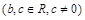 ,且
,且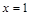 为
为 的极值点.
的极值点.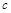 表示);
表示);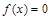 恰有两解,求实数
恰有两解,求实数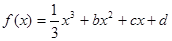 ,设曲线
,设曲线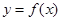 在与
在与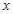 轴交点处的切线为
轴交点处的切线为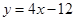 ,
,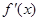 为
为 的导函数,满足
的导函数,满足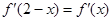 .
.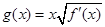 ,
,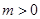 ,求函数
,求函数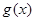 在
在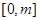 上的最大值;
上的最大值; ,
, ,
, 所围成的平面图形的面积。
所围成的平面图形的面积。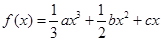 .(
.(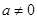 )
) 有三个零点
有三个零点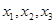 ,且
,且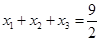 ,
,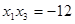 ,求函数
,求函数  的单调区间;
的单调区间; 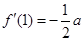 ,
,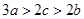 ,试问:导函数
,试问:导函数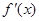 在区间(0,2)内是否有零点,并说明理由.
在区间(0,2)内是否有零点,并说明理由.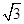 ,求
,求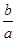 的取值范围.
的取值范围. .
.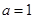 时,试判断
时,试判断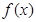 的单调性并给予证明;
的单调性并给予证明;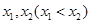 .
.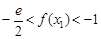 。 (注:
。 (注: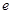 是自然对数的底数)
是自然对数的底数) (a为实常数).
(a为实常数).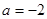 ,求证:函数
,求证:函数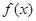 在(1,+.∞)上是增函数;
在(1,+.∞)上是增函数;  值;
值;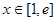 ,使得
,使得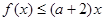 成立,求实数a的取值范围.
成立,求实数a的取值范围. ,函数
,函数 的最小值为
的最小值为 ,
, 时,求
时,求 同时满足下列条件:①
同时满足下列条件:① ;②当
;②当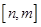 时,值域为
时,值域为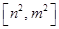
 ?若存在,求出
?若存在,求出