题目内容
(本小题满分12分)已知函数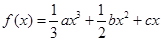 .(
.(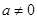 )
)
(1)若函数 有三个零点
有三个零点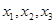 ,且
,且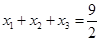 ,
,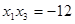 ,求函数
,求函数  的单调区间;
的单调区间;
(2)若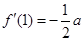 ,
,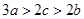 ,试问:导函数
,试问:导函数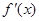 在区间(0,2)内是否有零点,并说明理由.
在区间(0,2)内是否有零点,并说明理由.
(3)在(Ⅱ)的条件下,若导函数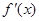 的两个零点之间的距离不小于
的两个零点之间的距离不小于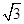 ,求
,求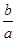 的取值范围.
的取值范围.
(1)当 时,
时, 的单调递减区间是(1,4),单调递增区间是
的单调递减区间是(1,4),单调递增区间是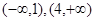 。当
。当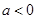 时,
时, 的单调递增区间是(1,4),单调递减区间是
的单调递增区间是(1,4),单调递减区间是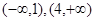 (4分)(2)导函数
(4分)(2)导函数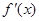 在区间(0,2)内至少有一个零点.(3)
在区间(0,2)内至少有一个零点.(3) .
.
解析试题分析:(1)因为 ,又
,又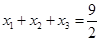 ,
, 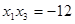
则 ……… (1分)
……… (1分)
因为x1,x3是方程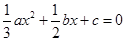 的两根,则
的两根,则 ,
,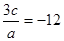 ,.即
,.即 …… (2分)
…… (2分)
从而: ,
,
所以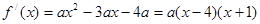 .
.
令 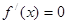 解得:
解得: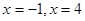 … ……… (3分)
… ……… (3分)
当 时,
时, 的单调递减区间是(1,4),单调递增区间是
的单调递减区间是(1,4),单调递增区间是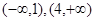 。
。
当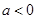 时,
时, 的单调递增区间是(1,4),单调递减区间是
的单调递增区间是(1,4),单调递减区间是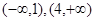 (4分)
(4分)
(2)因为 ,
,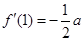 ,所以
,所以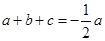 ,
,
即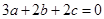 .
.
因为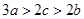 ,所以
,所以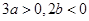 ,即
,即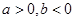 . (5分)
. (5分)
于是 ,
, ,
, .
.
①当 时,因为
时,因为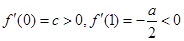 ,
,
则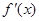 在区间
在区间 内至少有一个零点. (6分)
内至少有一个零点. (6分)
②当 时,因为
时,因为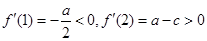 ,
,
则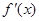 在区间(1,2)内至少有一零点.
在区间(1,2)内至少有一零点.
故导函数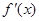 在区间(0,2)内至少有一个零点. (8分)
在区间(0,2)内至少有一个零点. (8分)
(3)设m,n是导函数 的两个零点,则
的两个零点,则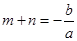 ,
,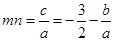 .
.
所以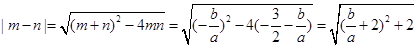 .
.
由已知, ,则
,则 ,即
,即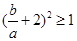 .
.
所以 ,即
,即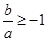 或
或 . (10分)
. (10分)
又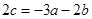 ,
,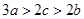 ,所以
,所以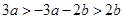 ,即
,即 .
.
因为 ,所以
,所以 .
.
综上分析,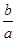 的取值范围是
的取值范围是 . (12分)
. (12分)
考点:本题考查了导数的运用
点评:可导函数的极值点都是导数等于零的点,求出结果要带回去检验,求函数的单调区间都是转化为导数与0的大小关系进行确定,导数大于0,原函数递增,导函数小于0,则原函数递减,特别是函数含字母时,要注意字母对解不等式的影响,有时需要分类讨论

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目

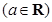 .
.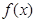 在定义域内的极值点的个数;
在定义域内的极值点的个数;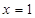 处取得极值,对
处取得极值,对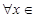
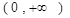 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.  (2)
(2)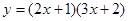
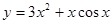 (4)
(4)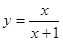

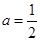 ,求
,求 的单调区间;
的单调区间; ≥0时
≥0时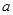 的取值范围.
的取值范围. (a>0,b,cÎR),曲线
(a>0,b,cÎR),曲线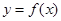 在点P(0,f (0))处的切线方程为
在点P(0,f (0))处的切线方程为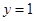 .
.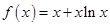 .
. 的图像在点
的图像在点 处的切线方程;
处的切线方程;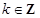 ,且
,且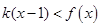 对任意
对任意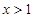 恒成立,求
恒成立,求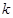 的最大值;
的最大值; .
.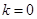 ,求
,求 的最小值;
的最小值;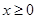 时
时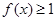 ,求实数
,求实数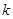 的取值范围.
的取值范围.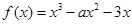
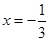 是
是 的极值点,求
的极值点,求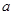 ]上的最大值;
]上的最大值; )上是增函数,求实数
)上是增函数,求实数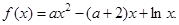
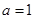 时,求曲线
时,求曲线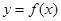 在点
在点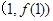 处的切线方程;
处的切线方程;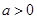 时,若
时,若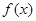 在区间
在区间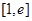 上的最小值为-2,求
上的最小值为-2,求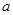 的取值范围;
的取值范围;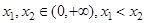 ,且
,且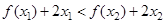 恒成立,求
恒成立,求