题目内容
已知关于 的函数
的函数
(Ⅰ)当 时,求函数
时,求函数 的极值;
的极值;
(Ⅱ)若函数 没有零点,求实数
没有零点,求实数 取值范围.
取值范围.
解:(Ⅰ) ,
, .
.
当 时,
时, ,
, 的情况如下表:
的情况如下表:
|
|
| 2 |
|
|
|
| 0 |
|
|
| ↘ | 极小值 | ↗ |
所以,当 时,函数
时,函数 的极小值为
的极小值为 .
.
(Ⅱ) .
.
①当 时,
时, 的情况如下表:
的情况如下表:
|
|
| 2 |
|
|
|
| 0 |
|
|
| ↘ | 极小值 | ↗ |
因为 ,
,
若使函数 没有零点,需且仅需
没有零点,需且仅需 ,解得
,解得 ,
,
所以此时 ;
;
②当 时,
时, 的情况如下表:
的情况如下表:
|
|
| 2 |
|
|
|
| 0 |
|
|
| ↗ | 极大值 | ↘ |
因为 ,且
,且 ,
,
所以此时函数 总存在零点.
总存在零点.
综上所述,所求实数 的取值范围是
的取值范围是 .
.

练习册系列答案
相关题目
已知向量 ,
, ,则“
,则“ ”是“
”是“ ∥
∥ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |







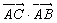 等于
等于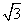 (C)2 (D)
(C)2 (D)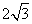
 的双曲线的两条渐近线互相垂直,则此双曲线的实轴长为 ( )
的双曲线的两条渐近线互相垂直,则此双曲线的实轴长为 ( ) (B)
(B) 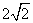 (D)
(D) 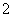
 满足条件
满足条件 则
则 的最大值是
的最大值是 B.
B.  C.
C. D.
D.
 过双曲线的左焦点
过双曲线的左焦点 ,且与以实轴为直径的圆相切,若直线
,且与以实轴为直径的圆相切,若直线 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 ,
, ,
, ,则
,则 ______.
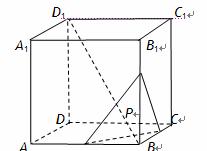
______.  的棱长为
的棱长为 ,动点P在对角线
,动点P在对角线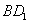 上,过点P作垂直于
上,过点P作垂直于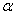 ,记这样得到的截面多边形(含三角形)的周长为y,设
,记这样得到的截面多边形(含三角形)的周长为y,设 x,则当
x,则当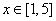 时,函数
时,函数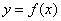 的值域为( )
的值域为( )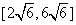 (B)
(B) (C)
(C) (D)
(D)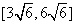
 ,
, ,
, ,则
,则 ( )
( ) B.
B.  C.
C.  D.
D. 