题目内容
15．设样本数据x1，x2，…，x10的均值和方差分别为1和4，若yi=xi+a（a为非零常数，i=1，2，…，10），则y1，y2，…，y10的均值和方差分别为（ ）| A． | 1+a，4 | B． | 1+a，4+a | C． | 1，4 | D． | 1，4+a |
分析 根据均值和方差的计算公式可求出结论．
解答 解：样本数据x1，x2，…，x10的均值为$\overline{x}$=1，方差为s2=4，
且yi=xi+a，
∴y1，y2，…，y10的均值为
$\overline{y}$=$\frac{1}{10}$（x1+x2+…+x10+10×a）=$\frac{1}{10}$（x1+x2+…+x10）+a=$\overline{x}$+a=1+a，
方差为s2=$\frac{1}{10}$[（x1+a-（$\overline{x}$+a）2+（x2+a-（$\overline{x}$+a）2+…+（x10+a-（$\overline{x}$+a）2]
=$\frac{1}{10}$[（x1-$\overline{x}$）2+（x2-$\overline{x}$）2+…+（x10-$\overline{x}$）2]
=s2=4．
故选：A．
点评 本题主要考查了样本数据的均值和方差的计算问题，利用定义或计算公式“变量y=ax+b，则Ey=aEx+b，Dy=a2Dx”，计算即可．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
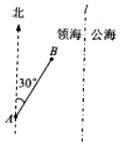一缉私艇巡航至距领海边界线l（一条南北方向的直线）3.8海里的A处，发现在其北偏东30°方向相距4海里的B处有一走私船正欲逃跑，缉私艇立即追击，已知缉私艇的最大航速是走私船最大航速的3倍，假设缉私艇和走私船均按直线方向以最大航速航行．
3．在△ABC中，角A，B，C的对边分别为a，b，c，且$\frac{cosB}{b}$=-$\frac{3cosC}{c}$，则角A的最大值是（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |
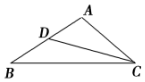如图所示，给出下列条件：