题目内容
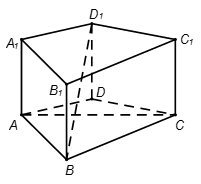
如图,在直三棱柱ABC—A1B1C1,AB=AC=1,∠BAC=90°,连结A1B与∠A1BC=60°.
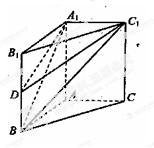
(Ⅰ)求证:AC⊥A1B;
(Ⅱ)设D是BB1的中点,求三棱锥D-A1BC1的体积.

(Ⅰ)求证:AC⊥A1B;
(Ⅱ)设D是BB1的中点,求三棱锥D-A1BC1的体积.
(Ⅰ)详见解析;(Ⅱ)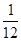
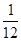
试题分析:(Ⅰ)借助直三棱柱的性质和线面垂直的性质定理证明
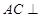 平面
平面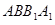 ,然后利用线面垂直的性质证明;(Ⅱ)证明
,然后利用线面垂直的性质证明;(Ⅱ)证明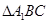 是正三角形,由
是正三角形,由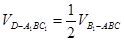 求解.
求解.试题解析:(Ⅰ)
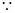 三棱柱
三棱柱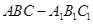 是直三棱柱,
是直三棱柱,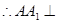 平面
平面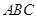 ,
,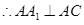 .
.又
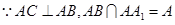 ,
,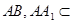 平面
平面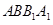
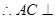 平面
平面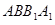 ,
,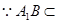 平面
平面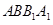 ,从而
,从而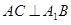 . (4分)
. (4分)(Ⅱ)连结
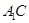 ,设
,设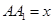 ,
,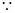
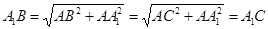 ,
,
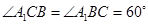 ,从而
,从而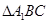 是正三角形,
是正三角形,
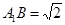 ,
,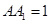 , (8分)
, (8分)又
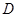 为
为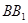 的中点.
的中点.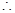
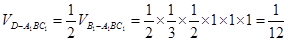 . (12分)
. (12分)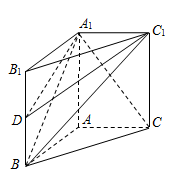

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中, 分别
分别 的中点.
的中点.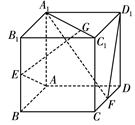
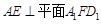 ;
;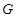 是靠近
是靠近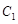 的
的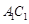 的四等分点,求证:
的四等分点,求证: .
.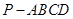 中,
中,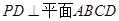 ,
,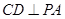 ,
, 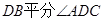 ,
,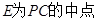 ,
,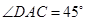 ,
,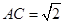 .
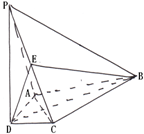
.
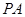 ∥
∥ ;
;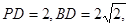 求四棱锥
求四棱锥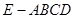 的体积
的体积 均为全等的直角梯形,且
均为全等的直角梯形,且 ,
, .
.
 平面
平面 ;
; 的余弦值.
的余弦值.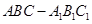 中,侧棱
中,侧棱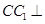 底面
底面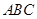 ,
,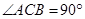 ,
,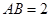 ,
,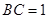 ,
,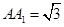 .
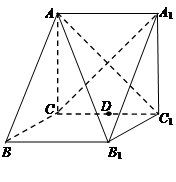
.
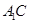
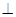 平面
平面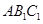 ;
;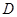 是棱
是棱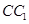 的中点,在棱
的中点,在棱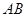 上是否存在一点
上是否存在一点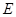 ,使
,使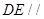 平面
平面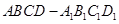 中,
中,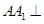 平面
平面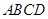 .
.
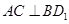 的充分条件,并给予证明;
的充分条件,并给予证明;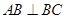 ,②
,②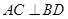 ;③
;③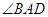 为锐角,求平面
为锐角,求平面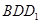 与平面
与平面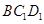 所成锐二面角
所成锐二面角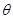 的取值范围.
的取值范围. ,则它的侧面与底面所成的(锐)二面角的大小为 .
,则它的侧面与底面所成的(锐)二面角的大小为 .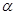 与平面
与平面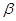 相交于直线
相交于直线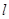 ,直线
,直线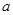 在平面
在平面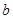 在平面
在平面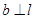 ,则“
,则“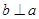 ”是“
”是“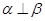 ”的( )
”的( )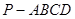 中,底面
中,底面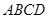 是边长为2的正方形,侧棱
是边长为2的正方形,侧棱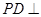 平面
平面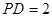 ,
, 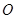 为底面对角线的交点,
为底面对角线的交点,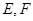 分别为棱
分别为棱 的中点
的中点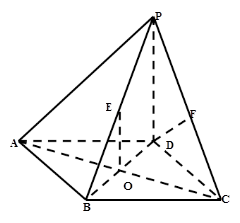
 //平面
//平面 ;
;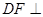 平面
平面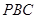 ;
;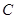 到平面
到平面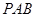 的距离。
的距离。