题目内容
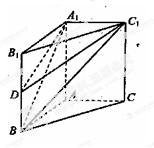
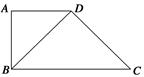
如图,在四棱锥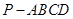 中,
中,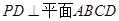 ,
,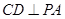 ,
, 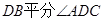 ,
,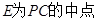 ,
,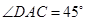 ,
,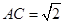 .
.
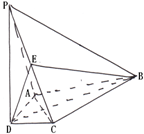
(Ⅰ)证明: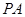 ∥
∥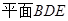 ;
;
(Ⅱ)若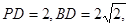 求四棱锥
求四棱锥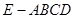 的体积
的体积
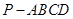 中,
中,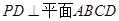 ,
,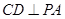 ,
, 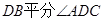 ,
,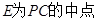 ,
,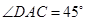 ,
,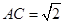 .
.
(Ⅰ)证明:
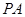 ∥
∥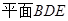 ;
;(Ⅱ)若
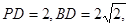 求四棱锥
求四棱锥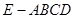 的体积
的体积(Ⅰ)见解析;(Ⅱ) .
.
 .
.试题分析:(Ⅰ)要证明线面平行只要证明线和平面内的一条直线平行或直线所在平面和此平面平行,此题我们用第一种证明,我们设
 ,连接EF,证明
,连接EF,证明 ∥
∥
 从而
从而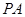 ∥
∥ ;(Ⅱ)先计算出四边形
;(Ⅱ)先计算出四边形 的面积,四棱锥的高为
的面积,四棱锥的高为 ,由体积公式可得
,由体积公式可得 .
.试题解析:(Ⅰ)设
 ,连接EF,
,连接EF,

 2分
2分∵
 ∴
∴ 3分
3分∵
 平分
平分
 为
为 中点,
中点, 为
为 中点,
中点,∴
 为
为 的中位线. 4分
的中位线. 4分∵
 ∥
∥ ,
,
∴
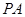 ∥
∥ . 6分
. 6分(Ⅱ)底面四边形
 的面积记为
的面积记为 ;
;
 . 9分
. 9分
 . 12分
. 12分
练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
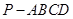 的底面
的底面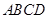 是正方形,棱
是正方形,棱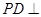 底面
底面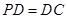 ,
,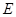 是
是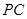 的中点.
的中点.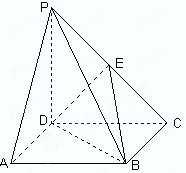
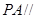 平面
平面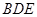 ;
;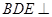 平面
平面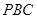 .
.
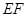 =;④垂直于截面.
=;④垂直于截面.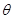 ,那么
,那么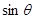 为 .
为 .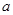 的等边三角形
的等边三角形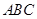 的中线
的中线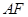 与中位线
与中位线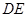 交于点
交于点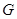 ,已知
,已知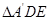 (
(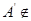 平面
平面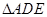 绕
绕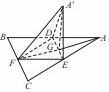
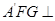 平面
平面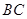 //平面
//平面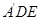 ;
;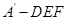 的体积最大值为
的体积最大值为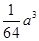 ;
;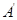 在平面
在平面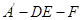 大小的范围是
大小的范围是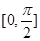 .
.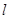 与平面
与平面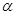 有公共点”是真命题,那么下列命题:
有公共点”是真命题,那么下列命题: