题目内容
4．满足不等式${（\frac{1}{3}）^x}＞\root{3}{9}$的实数x的取值范围为（ ）| A． | $x＞-\frac{2}{3}$ | B． | $x＞-\frac{3}{2}$ | C． | $x＜-\frac{2}{3}$ | D． | $x＜-\frac{3}{2}$ |
分析 化根式为分数指数幂，然后利用指数函数的单调性得答案．
解答 解：由（$\frac{1}{3}$）x＞$\root{3}{9}$，得3-x＞${3}^{\frac{2}{3}}$，
即-x＞$\frac{2}{3}$，即x＜-$\frac{2}{3}$，
故选：C．
点评 本题考查了指数不等式的解法，考查了根式与分数指数幂的互化，是基础题．
练习册系列答案
相关题目
8．若函数f（x）=lg（$\frac{2}{1-x}$+a）是奇函数，则使f（x）＜0的x的取值范围是（ ）
| A． | （0，1） | B． | （-1，0） | C． | （-∞，0） | D． | （-∞，0）∪（1，+∞） |
15．已知集合A={x|y=1n（1-x2）}，B={y|y=1n（1-x2）}，则CR（A∩B）=（ ）
| A． | （-∞，-1）∪（0，+∞） | B． | （-∞，-1]∪[0，+∞） | C． | （-1，0） | D． | [-1，0] |
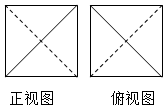已知某几何体的正视图和俯视图如图所示，则该几何体的侧视图是（ ）
