题目内容
17.$f(x)=asinx-b{log_3}(\sqrt{{x^2}+1}-x)+1$(a,b∈R),若f(lglog310)=5,则f(lglg3)的值是( )| A. | -5 | B. | -3 | C. | 3 | D. | 5 |
分析 设lglog310=m,则lglg3=-lglog310=-m.由f(lglog310)=5,得到asinm+b$lo{g}_{3}(\sqrt{{m}^{2}+1}-m)$=4,由此能求出结果.
解答 解:∵$f(x)=asinx-b{log_3}(\sqrt{{x^2}+1}-x)+1$(a,b∈R),
若f(lglog310)=5,∴设lglog310=m,
则lglg3=-lglog310=-m.
∵f(lglog310)=5,
$f(x)=asinx-b{log_3}(\sqrt{{x^2}+1}-x)+1$(a,b∈R),
∴f(m)=asinm+b$lo{g}_{3}(\sqrt{{m}^{2}+1}-m)+1$=5,
∴asinm+b$lo{g}_{3}(\sqrt{{m}^{2}+1}-m)$=4,
∴f(lglg3)=f(-m)=-(asinm+b$lo{g}_{3}(\sqrt{{m}^{2}+1}-m)$)+1=-4+1=-3.
故选:B.
点评 本题考查函数值求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.已知集合A={x|2x-1<0},B={x|0≤x≤1},那么A∩B等于( )
| A. | {x|x≥0} | B. | {x|x≤1} | C. | {x|0<x<$\frac{1}{2}$} | D. | {x|0≤x<$\frac{1}{2}$} |
5.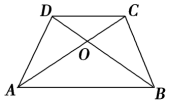 如图所示,梯形ABCD的对角线交于点O,则下列四个结论:
如图所示,梯形ABCD的对角线交于点O,则下列四个结论:
①△AOB∽△COD;
②△AOD∽△ACB;
③S△DOC:S△AOD=CD:AB;
④S△AOD=S△BOC.
其中正确的个数为( )
 如图所示,梯形ABCD的对角线交于点O,则下列四个结论:
如图所示,梯形ABCD的对角线交于点O,则下列四个结论:①△AOB∽△COD;
②△AOD∽△ACB;
③S△DOC:S△AOD=CD:AB;
④S△AOD=S△BOC.
其中正确的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
2.已知△ABC的顶点A(0,-4)、B(0,4),且4(sinB-sinA)=3sinC,则顶点C的轨迹方程是( )
| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{7}$=1(x>3) | B. | $\frac{{x}^{2}}{7}$-$\frac{{y}^{2}}{9}$=1(x<-7) | C. | $\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{7}$=1(y>3) | D. | $\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{7}$=1(y<-3) |
9.设全集U=R,集合A={x|x-1≤1},集合B={y|y=2x,x<1},则A∩(∁UB)=( )
| A. | {x|0<x<2} | B. | ∅ | C. | {0,2} | D. | {x|x≤0或x=2} |