题目内容
已知{an}是等比数列,a3,a8是关于x的方程x2-2xsinα-
sinα=0的两根,且(a3+a8)2=2a2a9+6,则锐角α的值为( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:数列与函数的综合,等比数列的性质
专题:等差数列与等比数列
分析:由已知条件推导出a3+a8=2sinα,a3•a8=a2a9=-2,由(a3+a8)2=2a2a9+6,得4sin2α=2,由此能求出锐角α的值.
解答:
解:∵{an}是等比数列,a3和a8是关于x的方程x2-2xsinα-2=0的两根,
∴a3+a8=2sinα,a3•a8=a2a9=-2,
∵(a3+a8)2=2a2a9+6,
∴4sin2α=2,即sin2α=
,
sinα=±
∴锐角α的值为45°.
故选:B.
∴a3+a8=2sinα,a3•a8=a2a9=-2,
∵(a3+a8)2=2a2a9+6,
∴4sin2α=2,即sin2α=
| 1 |
| 2 |
sinα=±
| ||
| 2 |
∴锐角α的值为45°.
故选:B.
点评:本题考查锐角的大小的求法,是基础题,解题时要认真审题,注意等比数列的性质的灵活运用.

练习册系列答案
相关题目
函数f(x)=-2x+ax3,若f′(2)=1,则a=( )
| A、4 | ||
B、
| ||
| C、-4 | ||
D、-
|
若
(2x-3x2)dx=0,则k=( )
| ∫ | k 0 |
| A、1 | B、0 |
| C、0或1 | D、以上都不对 |
已知{an}是等差数列,a1+a2=4,a7+a8=28,则该数列前8项和S8等于( )
| A、72 | B、64 |
| C、100 | D、120 |
| sin2600° |
A、±
| ||||
B、
| ||||
C、-
| ||||
D、
|
数列{an}满足:a1a2a3…an=
,则a2013=( )
| 1 |
| n |
A、
| ||
B、
| ||
C、
| ||
D、
|
设f(x)=
x3+ax2+5x+6在区间[1,3]上单调函数,则实数a的取值范围为( )
| 1 |
| 3 |
A、[-
| ||
| B、(-∞,-3] | ||
C、[-3,
| ||
D、(-∞,-3]∪[-
|
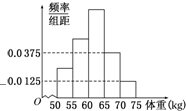 如图是某学校抽取的学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为10,则抽取的学生人数为( )
如图是某学校抽取的学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为10,则抽取的学生人数为( )