题目内容
直线l过点P(-2,0)且倾斜角为150°以直角坐标系的原点为极点,x轴正方向为极轴建立极坐标系,曲线C的极坐标方程ρ2-2ρcosθ=15.
(Ⅰ)写出直线l的参数方程和曲线C的直角坐标方程;
(Ⅱ)直线l交曲线C于A、B两点,求|PA|•|PB|的值.
(Ⅰ)写出直线l的参数方程和曲线C的直角坐标方程;
(Ⅱ)直线l交曲线C于A、B两点,求|PA|•|PB|的值.
考点:简单曲线的极坐标方程,两点间的距离公式
专题:坐标系和参数方程
分析:(I)由直线l过点P(-2,0)且倾斜角为150°,由tan150°=
,即可得出其参数方程为
.把
代入曲线C的极坐标方程即可得出直角坐标方程.
(II)把直线l参数方程为
代入曲线C的方程可得t2-3t-7=0,利用|PA|•|PB|=|t1t2|即可得出.
| sin150° |
| cos150° |
|
|
(II)把直线l参数方程为
|
解答:
解:(I)由直线l过点P(-2,0)且倾斜角为150°,其参数方程为
.
曲线C的极坐标方程ρ2-2ρcosθ=15化为x2+y2-2x=15.
(II)把直线l参数方程为
代入曲线C的方程可得t2-3t-7=0,
∴t1t2=-7.
∴|PA|•|PB|=|t1t2|=7.
|
曲线C的极坐标方程ρ2-2ρcosθ=15化为x2+y2-2x=15.
(II)把直线l参数方程为
|
∴t1t2=-7.
∴|PA|•|PB|=|t1t2|=7.
点评:本题考查了直线的参数方程化为普通方程、极坐标方程化为直角坐标方程、参数方程的应用,考查了计算能力,属于基础题.

练习册系列答案
相关题目
若方程y2-x2lga=
-a表示焦点在x轴上的椭圆,则a的取值范围是( )
| 1 |
| 3 |
A、(0 ,
| ||||
B、(
| ||||
C、(0 ,
| ||||
D、(
|
| ∫ | 1 0 |
| A、e+cos1 |
| B、e-cos1 |
| C、x-sin1 |
| D、e+sin1 |
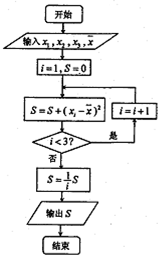
执行如图的程序框图,输出的T=( )


| A、12 | B、20 | C、42 | D、30 |