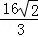题目内容
已知函数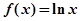 ,
,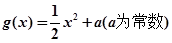 ,直线
,直线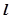 与 函数
与 函数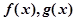 的图像都相切,且
的图像都相切,且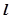 与函数
与函数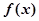 图像的切点的横坐标为1,则
图像的切点的横坐标为1,则 的值为 ( )
的值为 ( )
| A.1 | B.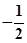 | C.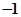 | D.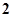 |
B
解析试题分析:对 分别求导得
分别求导得 ,且
,且 ,则直线斜率
,则直线斜率 ,设直线为
,设直线为 且与
且与 的切点为
的切点为 ,则
,则 ,直线方程为
,直线方程为 与
与 联立即
联立即 ,
, ,因为
,因为 ,即
,即 ,解得
,解得 .
.
考点:利用导数解决解析几何问题.

练习册系列答案
相关题目
函数 在区间
在区间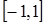 上的最大值是( )
上的最大值是( )
A. | B.0 | C.2 | D.4 |
定义在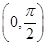 上的函数
上的函数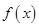 ,其导函数是
,其导函数是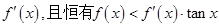 成立,则
成立,则
A.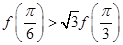 | B.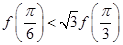 |
C.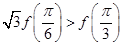 | D.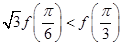 |
函数y=xsinx+cosx在下面哪个区间内是增函数( )
A. | B. | C. | D. |
若a>0, b>0, 且函数f(x)=4x3-ax2-2bx+2在x=1处有极值,则ab的最大值等于( )
| A.2 | B.3 | C.6 | D.9 |
[2013·江西高考]若S1= ,S2=
,S2= ,S3=
,S3= ,则S1,S2,S3的大小关系为( )
,则S1,S2,S3的大小关系为( )
| A.S1<S2<S3 | B.S2<S1<S3 | C.S2<S3<S1 | D.S3<S2<S1 |
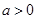 时,函数
时,函数 的图象大致是
的图象大致是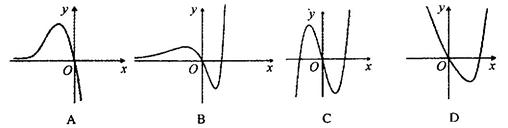
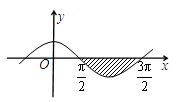
 的一段图象与x轴围成的封闭图形,那么这个阴影区域的面积是( )
的一段图象与x轴围成的封闭图形,那么这个阴影区域的面积是( )