题目内容
7.若二项式(2-x)n(n∈N*)的展开式中所有项的系数的绝对值之和是a,所有项的二项式系数之和是b,则$\frac{b}{a}+\frac{a}{b}$的最小值是( )| A. | 2 | B. | $\frac{13}{6}$ | C. | $\frac{7}{3}$ | D. | $\frac{15}{6}$ |
分析 取x=-1求得a,由二项式系数的性质求得b,然后利用函数的单调性求得$\frac{b}{a}+\frac{a}{b}$的最小值.
解答 解:取x=-1,得a=3n,
又b=2n,∴$\frac{b}{a}=\frac{{2}^{n}}{{3}^{n}}=(\frac{2}{3})^{n}$,
∴$\frac{b}{a}+\frac{a}{b}$=$(\frac{2}{3})^{n}+(\frac{3}{2})^{n}$≥$\frac{2}{3}+\frac{3}{2}=\frac{13}{6}$.
故选:B.
点评 本题考查了二项式定理、函数的单调性,考查了计算能力,属于基础题.

练习册系列答案
相关题目
18.阅读如图所示的程序框图,若输出的数据为58,则判断框中应填入的条件为( )


| A. | k≤3 | B. | k≤4 | C. | k≤5 | D. | k≤6 |
15.定义在区间[a,b](b>a)上的函数$f(x)=\frac{1}{2}sinx-\frac{{\sqrt{3}}}{2}cosx$的值域是$[-\frac{1}{2},1]$,则b-a的最大值M和最小值m分别是( )
| A. | $m=\frac{π}{6},M=\frac{π}{3}$ | B. | $m=\frac{π}{3},M=\frac{2π}{3}$ | C. | $m=\frac{4π}{3},M=2π$ | D. | $m=\frac{2π}{3},M=\frac{4π}{3}$ |
12.已知i为虚数单位,复数z满足1+i+(1+i)2z=(1-i)2,则复数z的虚部为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{2}i$ | C. | $\frac{3}{2}$ | D. | $-\frac{3}{2}$ |
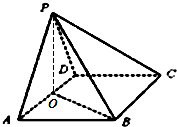 如图,在四棱锥P-ABCD中,底面ABCD为菱形且∠DAB=60°,O为AD中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形且∠DAB=60°,O为AD中点.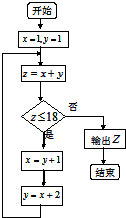
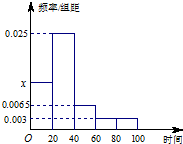 某学校随机抽取100名学生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].则该校学生上学所需时间的均值估计为33.6.(精确到1分钟)
某学校随机抽取100名学生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].则该校学生上学所需时间的均值估计为33.6.(精确到1分钟)