题目内容
2.已知三棱柱ABC-A1B1C1的侧棱和底面垂直,且所有棱长都相等,若该三棱柱的各顶点都在球O的表面上,且球O的表面积为7π,则此三棱柱的体积为$\frac{9}{4}$.分析 通过球的内接体,说明几何体的中心是球的直径,由球的表面积求出球的半径,设出三棱柱的底面边长,通过解直角三角形求得a,然后由棱柱的体积公式得答案.
解答 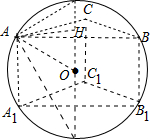 解:如图,
解:如图,
∵三棱柱ABC-A1B1C1的所有棱长都相等,6个顶点都在球O的球面上,
∴三棱柱为正三棱柱,且其中心为球的球心,设为O,
再设球的半径为r,由球O的表面积为7π,得4πr2=7π,∴r=$\frac{\sqrt{7}}{2}$.
设三棱柱的底面边长为a,则上底面所在圆的半径为$\frac{\sqrt{3}}{3}$a,且球心O到上底面中心H的距离OH=$\frac{a}{2}$,
∴r2=($\frac{a}{2}$)2+($\frac{\sqrt{3}}{3}$a)2,即r=$\sqrt{\frac{7}{12}}$a,
∴a=$\sqrt{3}$.
则三棱柱的底面积为S=$\frac{\sqrt{3}}{4}×{(\sqrt{3})}^{2}$=$\frac{3\sqrt{3}}{4}$.
∴${V}_{ABC-{A}_{1}{B}_{1}{C}_{1}}$=$\frac{3\sqrt{3}}{4}×\sqrt{3}$=$\frac{9}{4}$.
故答案为:$\frac{9}{4}$.
点评 本题考查球的内接体与球的关系,球的半径的求解,考查计算能力,是中档题.

练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
17.如图是一建筑物的三视图(单位:米),现需将其外壁用油漆刷一遍,若每平方米用漆α千克,则共需油漆的总量为( )
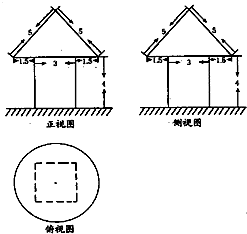

| A. | (48+36π)α千克 | B. | (39+24π)α千克 | C. | (36+36π)α千克 | D. | (36+30π)α千克 |
7.若二项式(2-x)n(n∈N*)的展开式中所有项的系数的绝对值之和是a,所有项的二项式系数之和是b,则$\frac{b}{a}+\frac{a}{b}$的最小值是( )
| A. | 2 | B. | $\frac{13}{6}$ | C. | $\frac{7}{3}$ | D. | $\frac{15}{6}$ |
11.某班主任对全班50名学生学习积极性和参加社团活动情况进行调查,统计数据表1
(1)如果随机从该班抽查一名学生,抽到参加社团活动的学生的概率是多少?抽到不参加社团活动且学习积极性一般的学生的概率是多少?
(2)运用独立检验的思想方法分析:学生的学习积极性与参加社团活动情况是否有关系?并说明理由.
${Χ^2}=\frac{{n{{({{n_{11}}{n_{22}}-{n_{12}}{n_{21}}})}^2}}}{{{n_{1+}}{n_{2+}}{n_{+1}}{n_{+2}}}}$
(1)抽到参加社团活动的学生的概率是$\frac{11}{25}$,抽到不参加社团活动且学习积极性一般的学生的概率是$\frac{2}{5}$;
(2)有99.9%的把握认为学生的学习积极性与参加社团活动的态度有关系.
| 参加社团活动 | 不参加社团活动 | 合计 | |
| 学习积极性高 | 17 | 8 | 25 |
| 学习积极性一般 | 5 | 20 | 25 |
| 合计 | 22 | 28 | 50 |
(2)运用独立检验的思想方法分析:学生的学习积极性与参加社团活动情况是否有关系?并说明理由.
| P(Χ2≥k) | 0.05 | 0.01 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
(1)抽到参加社团活动的学生的概率是$\frac{11}{25}$,抽到不参加社团活动且学习积极性一般的学生的概率是$\frac{2}{5}$;
(2)有99.9%的把握认为学生的学习积极性与参加社团活动的态度有关系.