题目内容
16.在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系.若点P为直线ρcosθ-ρsinθ-4=0上一点,点Q为曲线$\left\{\begin{array}{l}{x=t}\\{y=\frac{1}{4}{t}^{2}}\end{array}\right.$(t为参数)上一点,则|PQ|的最小值为$\frac{3\sqrt{2}}{2}$.分析 直线ρcosθ-ρsinθ-4=0化为x-y-4=0,曲线$\left\{\begin{array}{l}{x=t}\\{y=\frac{1}{4}{t}^{2}}\end{array}\right.$(t为参数)化为x2=4y.设与此抛物线相切且与直线x-y-4=0平行的直线方程为x-y+m=0,代入抛物线方程可化为x2-4x+4m=0,利用△=0,解得m.可得切点Q.求出点Q到直线l的距离d即可得出.
解答 解:直线ρcosθ-ρsinθ-4=0化为x-y-4=0,
曲线$\left\{\begin{array}{l}{x=t}\\{y=\frac{1}{4}{t}^{2}}\end{array}\right.$(t为参数)化为x2=4y.
设与此抛物线相切且与直线x-y-4=0平行的直线方程为x-y+m=0,
联立$\left\{\begin{array}{l}{x-y+m=0}\\{{x}^{2}=4y}\end{array}\right.$,化为x2-4x+4m=0,
∵△=16-16m=0,解得m=1.
可得切点Q(2,1).
∴点Q到直线l的距离d=$\frac{|2-1-4|}{\sqrt{2}}$=$\frac{3\sqrt{2}}{2}$.
∴|PQ|的最小值为$\frac{3\sqrt{2}}{2}$.
故答案为:$\frac{3\sqrt{2}}{2}$.
点评 本题考查了抛物线参数方程、直角坐标方程与极坐标方程互化、直线与抛物线相切、点到直线的距离公式,考查了推理能力与计算能力,属于中档题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.若二项式(2-x)n(n∈N*)的展开式中所有项的系数的绝对值之和是a,所有项的二项式系数之和是b,则$\frac{b}{a}+\frac{a}{b}$的最小值是( )
| A. | 2 | B. | $\frac{13}{6}$ | C. | $\frac{7}{3}$ | D. | $\frac{15}{6}$ |
11.某班主任对全班50名学生学习积极性和参加社团活动情况进行调查,统计数据表1
(1)如果随机从该班抽查一名学生,抽到参加社团活动的学生的概率是多少?抽到不参加社团活动且学习积极性一般的学生的概率是多少?
(2)运用独立检验的思想方法分析:学生的学习积极性与参加社团活动情况是否有关系?并说明理由.
${Χ^2}=\frac{{n{{({{n_{11}}{n_{22}}-{n_{12}}{n_{21}}})}^2}}}{{{n_{1+}}{n_{2+}}{n_{+1}}{n_{+2}}}}$
(1)抽到参加社团活动的学生的概率是$\frac{11}{25}$,抽到不参加社团活动且学习积极性一般的学生的概率是$\frac{2}{5}$;
(2)有99.9%的把握认为学生的学习积极性与参加社团活动的态度有关系.
| 参加社团活动 | 不参加社团活动 | 合计 | |
| 学习积极性高 | 17 | 8 | 25 |
| 学习积极性一般 | 5 | 20 | 25 |
| 合计 | 22 | 28 | 50 |
(2)运用独立检验的思想方法分析:学生的学习积极性与参加社团活动情况是否有关系?并说明理由.
| P(Χ2≥k) | 0.05 | 0.01 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
(1)抽到参加社团活动的学生的概率是$\frac{11}{25}$,抽到不参加社团活动且学习积极性一般的学生的概率是$\frac{2}{5}$;
(2)有99.9%的把握认为学生的学习积极性与参加社团活动的态度有关系.
8.已知双曲线的顶点与焦点分别是椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的焦点与顶点,若双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,则椭圆的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
5.一个几何体按比例绘制的三视图如图所示(单位:m),则该几何体的体积为( )
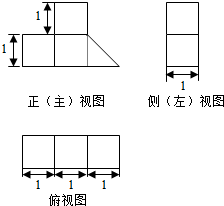

| A. | $\frac{7}{3}$ m3 | B. | $\frac{9}{2}$ m3 | C. | $\frac{9}{4}$ m3 | D. | $\frac{7}{2}$ m3 |
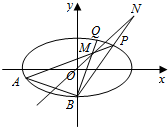 如图,已知椭圆C:$\frac{x^2}{2}$+y2=1,点B坐标为(0,-1),过点B的直线交椭圆C于y轴左侧另外一点A,且线段AB的中点E在直线y=x上.
如图,已知椭圆C:$\frac{x^2}{2}$+y2=1,点B坐标为(0,-1),过点B的直线交椭圆C于y轴左侧另外一点A,且线段AB的中点E在直线y=x上.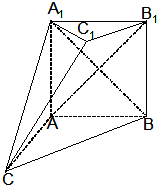 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,△A1CB是等边三角形,AC=AB=1,B1C1∥BC,BC=2B1C1
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,△A1CB是等边三角形,AC=AB=1,B1C1∥BC,BC=2B1C1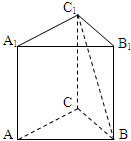 如图,在三棱柱ABC-A1B1C1中,底面是边长为1的正三角形,AA1⊥平面ABC,AA1=$\sqrt{2}$,则BC1与侧面ACC1A1所成的角的大小为$\frac{π}{6}$.
如图,在三棱柱ABC-A1B1C1中,底面是边长为1的正三角形,AA1⊥平面ABC,AA1=$\sqrt{2}$,则BC1与侧面ACC1A1所成的角的大小为$\frac{π}{6}$.