题目内容
19.执行如图所示的程序,则输出的结果为24.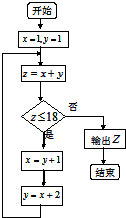
分析 由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量Z的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.
解答 解:第一次执行循环体后,z=2,满足继续循环的条件,x=2,y=4;
再次执行循环体后,z=6,满足继续循环的条件,x=5,y=7;
再次执行循环体后,z=12,满足继续循环的条件,x=8,y=10;
再次执行循环体后,z=18,满足继续循环的条件,x=11,y=13;
再次执行循环体后,z=24,不满足继续循环的条件,
故输出的结果为:24,
故答案为:24.
点评 本题考查的知识点是程序框图,当循环的次数不多,或有规律时,常采用模拟循环的方法解答.

练习册系列答案
相关题目
7.若二项式(2-x)n(n∈N*)的展开式中所有项的系数的绝对值之和是a,所有项的二项式系数之和是b,则$\frac{b}{a}+\frac{a}{b}$的最小值是( )
| A. | 2 | B. | $\frac{13}{6}$ | C. | $\frac{7}{3}$ | D. | $\frac{15}{6}$ |
11.某班主任对全班50名学生学习积极性和参加社团活动情况进行调查,统计数据表1
(1)如果随机从该班抽查一名学生,抽到参加社团活动的学生的概率是多少?抽到不参加社团活动且学习积极性一般的学生的概率是多少?
(2)运用独立检验的思想方法分析:学生的学习积极性与参加社团活动情况是否有关系?并说明理由.
${Χ^2}=\frac{{n{{({{n_{11}}{n_{22}}-{n_{12}}{n_{21}}})}^2}}}{{{n_{1+}}{n_{2+}}{n_{+1}}{n_{+2}}}}$
(1)抽到参加社团活动的学生的概率是$\frac{11}{25}$,抽到不参加社团活动且学习积极性一般的学生的概率是$\frac{2}{5}$;
(2)有99.9%的把握认为学生的学习积极性与参加社团活动的态度有关系.
| 参加社团活动 | 不参加社团活动 | 合计 | |
| 学习积极性高 | 17 | 8 | 25 |
| 学习积极性一般 | 5 | 20 | 25 |
| 合计 | 22 | 28 | 50 |
(2)运用独立检验的思想方法分析:学生的学习积极性与参加社团活动情况是否有关系?并说明理由.
| P(Χ2≥k) | 0.05 | 0.01 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
(1)抽到参加社团活动的学生的概率是$\frac{11}{25}$,抽到不参加社团活动且学习积极性一般的学生的概率是$\frac{2}{5}$;
(2)有99.9%的把握认为学生的学习积极性与参加社团活动的态度有关系.
8.已知双曲线的顶点与焦点分别是椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的焦点与顶点,若双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,则椭圆的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
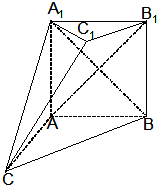 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,△A1CB是等边三角形,AC=AB=1,B1C1∥BC,BC=2B1C1
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,△A1CB是等边三角形,AC=AB=1,B1C1∥BC,BC=2B1C1