题目内容
7.贝已知向量$\overrightarrow{a}$=(1,x),$\overrightarrow{b}$=(x-3,2),且$\overrightarrow{a}⊥\overrightarrow{b}$.(1)求x的值;
(2)试确定实数k的值,使k$\overrightarrow{a}+\overrightarrow{b}$与$\overrightarrow{a}-2\overrightarrow{b}$平行.
分析 (1)根据题意,若$\overrightarrow{a}⊥\overrightarrow{b}$,则有$\overrightarrow{a}$•$\overrightarrow{b}$=0,由向量的数量积坐标计算公式可得$\overrightarrow{a}$•$\overrightarrow{b}$=(x-3)+2x=3x-3=0,解可得x的值;
(2)由(1)可得x的值,则可得向量$\overrightarrow{a}$、$\overrightarrow{b}$的坐标,计算可得k$\overrightarrow{a}+\overrightarrow{b}$与$\overrightarrow{a}-2\overrightarrow{b}$的坐标,由向量平行的坐标表示方法计算可得答案.
解答 解:(1)根据题意,向量$\overrightarrow{a}$=(1,x),$\overrightarrow{b}$=(x-3,2),
若$\overrightarrow{a}⊥\overrightarrow{b}$,则有$\overrightarrow{a}$•$\overrightarrow{b}$=(x-3)+2x=3x-3=0,
解可得x=1,
(2)由(1)可得x=1,
则$\overrightarrow{a}$=(1,1),$\overrightarrow{b}$=(-2,2),
k$\overrightarrow{a}+\overrightarrow{b}$=(k-2,k+2),$\overrightarrow{a}-2\overrightarrow{b}$=(5,-3),
若k$\overrightarrow{a}+\overrightarrow{b}$与$\overrightarrow{a}-2\overrightarrow{b}$平行,则有(-3)(k-2)=5(k+2),
解可得k=$\frac{1}{2}$;
故k=$\frac{1}{2}$.
点评 本题考查平面向量的坐标计算,关键是求出x的值.

 阅读快车系列答案
阅读快车系列答案| A. | y=±4x | B. | y=±$\frac{1}{4}$x | C. | y=±2x | D. | y=±$\frac{1}{2}$x |
| A. | (-3,0) | B. | (-3,3) | C. | (0,3) | D. | (0,+∞) |
| A. | -2 | B. | -3或3 | C. | -2或2 | D. | -3或-2 |
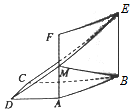 如图所示,在直角梯形ABCD中,AD∥BC,AD⊥DC,BC=2AD=2DC,四边形ABEF是正方形,且平面ABEF⊥平面ABCD,M为AF的中点,
如图所示,在直角梯形ABCD中,AD∥BC,AD⊥DC,BC=2AD=2DC,四边形ABEF是正方形,且平面ABEF⊥平面ABCD,M为AF的中点,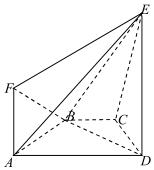 如图所示,等腰梯形ABCD的底角 A等于60°,直角梯形 ADEF所在的平面垂直于平面ABCD,∠EDA=90°,且ED=AD=2AB=2AF.
如图所示,等腰梯形ABCD的底角 A等于60°,直角梯形 ADEF所在的平面垂直于平面ABCD,∠EDA=90°,且ED=AD=2AB=2AF.