题目内容
给定函数f(x)=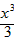 -ax2+(a2-1)x和g(x)=x+
-ax2+(a2-1)x和g(x)=x+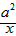 。
。
(1)求证:f(x)总有两个极值点;
(2)若f(x)和g(x)有相同的极值点,求a的值。
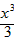 -ax2+(a2-1)x和g(x)=x+
-ax2+(a2-1)x和g(x)=x+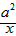 。
。(1)求证:f(x)总有两个极值点;
(2)若f(x)和g(x)有相同的极值点,求a的值。
解:(1)证明:因为f′(x)=x2-2ax+(a2-1)=[x-(a+ 1)]·[x-(a-1)],
令f′(x)=0,
解得x1=a+1,x2=a-1,
当x<a-1时f′(x)>0;
当a-1<x<a+1,f′(x)<0,
所以x=a-1为f(x)的一个极大值点,
同理可证x=a+1为f(x)的一个极小值点,
所以f(x)总有两个极值点;
(2)因为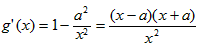 ,
,
令g′(x)=0,则x1=a,x2=-a,
因为f(x)和g(x)有相同的极值点,且x1=a和a+1,a-1不可能相等,
所以当-a=a+1时,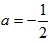 ;
;
当-a=a-1时,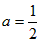 ,
,
经检验,当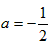 和
和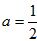 时,x1=a,x2=-a都是g(x) 的极值点。
时,x1=a,x2=-a都是g(x) 的极值点。
令f′(x)=0,
解得x1=a+1,x2=a-1,
当x<a-1时f′(x)>0;
当a-1<x<a+1,f′(x)<0,
所以x=a-1为f(x)的一个极大值点,
同理可证x=a+1为f(x)的一个极小值点,
所以f(x)总有两个极值点;
(2)因为
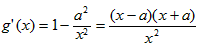 ,
,令g′(x)=0,则x1=a,x2=-a,
因为f(x)和g(x)有相同的极值点,且x1=a和a+1,a-1不可能相等,
所以当-a=a+1时,
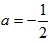 ;
;当-a=a-1时,
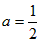 ,
,经检验,当
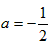 和
和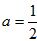 时,x1=a,x2=-a都是g(x) 的极值点。
时,x1=a,x2=-a都是g(x) 的极值点。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目