题目内容
【题目】在直角坐标系xOy中,直线l的参数方程为  (t为参数),以原点为极点,x轴正半轴为极轴建立极坐标系,⊙C的极坐标方程为ρ=2
(t为参数),以原点为极点,x轴正半轴为极轴建立极坐标系,⊙C的极坐标方程为ρ=2 ![]() sinθ. (Ⅰ)写出⊙C的直角坐标方程;
sinθ. (Ⅰ)写出⊙C的直角坐标方程;
(Ⅱ)P为直线l上一动点,当P到圆心C的距离最小时,求P的直角坐标.
【答案】解:(I)由⊙C的极坐标方程为ρ=2 ![]() sinθ. ∴ρ2=2
sinθ. ∴ρ2=2 ![]() ,化为x2+y2=
,化为x2+y2= ![]() ,
,
配方为 ![]() =3.
=3.
(II)设P 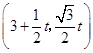 ,又C
,又C ![]() .
.
∴|PC|= ![]() =
= ![]() ≥2
≥2 ![]() ,
,
因此当t=0时,|PC|取得最小值2 ![]() .此时P(3,0)
.此时P(3,0)
【解析】(I)由⊙C的极坐标方程为ρ=2 ![]() sinθ.化为ρ2=2
sinθ.化为ρ2=2 ![]() ,把
,把 ![]() 代入即可得出;.(II)设P
代入即可得出;.(II)设P ![]() ,又C
,又C ![]() .利用两点之间的距离公式可得|PC|=
.利用两点之间的距离公式可得|PC|= ![]() ,再利用二次函数的性质即可得出.
,再利用二次函数的性质即可得出.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目