题目内容
【题目】为了培养学生的数学建模和应用能力,某校组织了一次实地测量活动,如图,假设待测量的树木 ![]() 的高度
的高度 ![]() ,垂直放置的标杆
,垂直放置的标杆 ![]() 的高度
的高度 ![]() ,仰角
,仰角 ![]() 三点共线),试根据上述测量方案,回答如下问题:
三点共线),试根据上述测量方案,回答如下问题: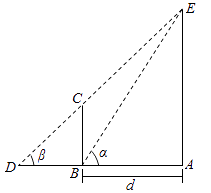
(1)若测得 ![]() ,试求
,试求 ![]() 的值;
的值;
(2)经过分析若干测得的数据后,大家一致认为适当调整标杆到树木的距离 ![]() (单位:)使
(单位:)使 ![]() 与
与 ![]() 之差较大时,可以提高测量的精确度.若树木的实际高为
之差较大时,可以提高测量的精确度.若树木的实际高为 ![]() ,试问
,试问 ![]() 为多少时,
为多少时, ![]() 最大?
最大?
【答案】
(1)解: ![]() ,同理:
,同理: ![]() ,
, ![]() .
.
![]() ,故得
,故得 ![]() ,
,
解得: ![]()
![]()

(2)解:由题设知 ![]() ,得
,得 ![]() ,
,

而 ![]() ,(当且仅当
,(当且仅当 ![]() =
= ![]() 时 取等号)
时 取等号)
故当 ![]() 时,
时, ![]() 最大.
最大.
因为 ![]() ,则
,则 ![]() ,
,
所以当 ![]() 时,
时, ![]() 最大.
最大.
【解析】(1)根据题意解三角形即可得出A B 、B D的代数式再利用A D A B = D B即可求出H。(2)先d分别表示出tanα、![]() ,再根据两角和公式求得 tan ( α β )的代数式整理成基本不等式的形式然后根据基本不等式求出该式的最大值进而可得 α β 有最大值求出即可。
,再根据两角和公式求得 tan ( α β )的代数式整理成基本不等式的形式然后根据基本不等式求出该式的最大值进而可得 α β 有最大值求出即可。
【考点精析】本题主要考查了基本不等式在最值问题中的应用的相关知识点,需要掌握用基本不等式求最值时(积定和最小,和定积最大),要注意满足三个条件“一正、二定、三相等”才能正确解答此题.

练习册系列答案
相关题目
【题目】某种商品价格与该商品日需求量之间的几组对照数据如表:
价格x(元/kg) | 10 | 15 | 20 | 25 | 30 |
日需求量y(kg) | 11 | 10 | 8 | 6 | 5 |
(1)求y关于x的线性回归方程;
(2)利用(1)中的回归方程,当价格x=40元/kg时,日需求量y的预测值为多少?
参考公式:线性回归方程 ![]() ,其中
,其中 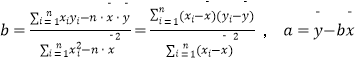 .
.
