题目内容
2.在△ABC中,B=135°,C=15°,a=5,则此三角形的最小边长为$\frac{5\sqrt{6}-5\sqrt{2}}{2}$,外接圆的面积为25π.分析 根据题意,由A、C的大小可得B=75°,由三角形的角边关系分析可得c为最小边;进而由正弦定理=,变形可得c=,代入数据计算可得答案.
解答 解:根据题意,在△ABC中,B=135°,C=15°,则A=180°-135°-15°=30°,
则有B>A>C,则c为最小边,
由正弦定理可得:c=$\frac{a•sinC}{sinA}$=$\frac{5×sin15°}{sin30°}$=$\frac{5\sqrt{6}-5\sqrt{2}}{2}$,外接圆的半径R=$\frac{a}{2sinA}$=$\frac{5}{2×\frac{1}{2}}$=5,
可得:外接圆的面积S=πR2=25π.
故答案为:$\frac{5\sqrt{6}-5\sqrt{2}}{2}$,25π.
点评 本题考查正弦定理的运用,注意要先求出A的值,由三角形角边关系分析出最小边,属于基础题.

练习册系列答案
相关题目
12. 如图,E,F分别是三棱锥P-ABC的棱AP,BC的中点,PC=AB=2,EF=$\sqrt{2}$,则异面直线AB与PC所成的角为( )
如图,E,F分别是三棱锥P-ABC的棱AP,BC的中点,PC=AB=2,EF=$\sqrt{2}$,则异面直线AB与PC所成的角为( )
 如图,E,F分别是三棱锥P-ABC的棱AP,BC的中点,PC=AB=2,EF=$\sqrt{2}$,则异面直线AB与PC所成的角为( )
如图,E,F分别是三棱锥P-ABC的棱AP,BC的中点,PC=AB=2,EF=$\sqrt{2}$,则异面直线AB与PC所成的角为( )| A. | 60° | B. | 45° | C. | 90° | D. | 30° |
17.函数f(x)=xlnx-1的零点所在区间为( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
14. 如图,在直三棱柱ABC-A1B1C1中,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成角的度数是( )
如图,在直三棱柱ABC-A1B1C1中,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成角的度数是( )
 如图,在直三棱柱ABC-A1B1C1中,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成角的度数是( )
如图,在直三棱柱ABC-A1B1C1中,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成角的度数是( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
1.设f(x)可导且下列各极限均存在,则( )成立.
| A. | $\underset{lim}{x→0}$$\frac{f(x)-f(0)}{x}$=f′(0) | B. | $\underset{lim}{h→0}$$\frac{f(a+2h)-f(a)}{h}$=f′(a) | ||
| C. | $\underset{lim}{△x→0}$$\frac{f({x}_{0})-f({x}_{0}-△x)}{△x}$=f′(x0) | D. | $\underset{lim}{△x→0}$$\frac{f({x}_{0}+△x)-f({x}_{0}-△x)}{2△x}$=f′(x0) |
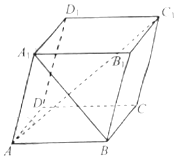 已知平行六面体ABCD-A1B1C1D1的底面ABCD为正方形,且∠A1AB=∠A1AD=60°,则当$\frac{{A}_{1}A}{AB}$=$\frac{\sqrt{17}-1}{4}$时,AC1⊥A1B.
已知平行六面体ABCD-A1B1C1D1的底面ABCD为正方形,且∠A1AB=∠A1AD=60°,则当$\frac{{A}_{1}A}{AB}$=$\frac{\sqrt{17}-1}{4}$时,AC1⊥A1B.