题目内容
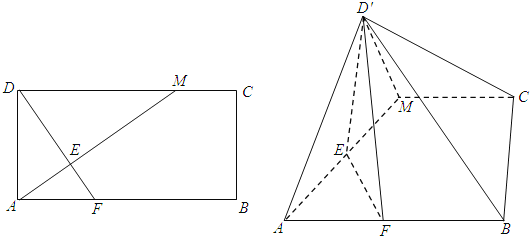
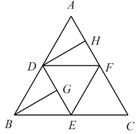
【题目】如图，在边长为4的正三角形ABC中，D，E，F分别为各边的中点，G，H分别为DE，AF的中点，将
沿DE，EF，DF折成正四面体
，则在此正四面体中，下列说法正确的是______．
异面直线PG与DH所成的角的余弦值为
；
；
与PD所成的角为
；
与EF所成角为
【答案】
【解析】
可证明
平面
,可得
正确；连接
,取中点
,异面直线
与
所成的角为
，由余弦定理可证明
正确；取
中点
，连接
，异面
与
所成的角为
，由余弦定理可得
不对；异面
与
所成角的为
，由余弦定理可得
不对，从而可得结果.
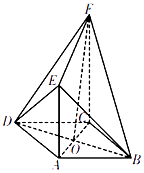
的边长为4，折成正四面体
后，如图
，E，F分别为各边的中点，G，H分别为DE，AF的中点，
，
；
连接FG，取中点M，可得
，
异面直线PG与DH所成的角的平角为；
，
连接MD，可得
．
；
在
中，
余弦定理：
；
对；
对；
取DF中点N，连接GN，NH，可得
异面GH与PD所成的角的平面角为，
由余弦定理，GH与PD所成的角不是
；不对；
异面PG与EF所成角的平面角为，
由余弦定理，可得PG与EF所成角不是
不对．
故答案为：．
练习册系列答案
相关题目
