题目内容
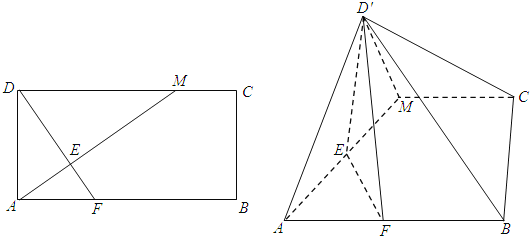
【题目】如图,在矩形ABCD中,![]() ,点M在边DC上,点F在边AB上,且
,点M在边DC上,点F在边AB上,且![]() ,垂足为E,若将
,垂足为E,若将![]() 沿AM折起,使点D位于
沿AM折起,使点D位于![]() 位置,连接
位置,连接![]() ,
,![]() 得四棱锥
得四棱锥![]() .
.
![]() Ⅰ
Ⅰ![]() 求证:
求证:![]() ;
;
![]() Ⅱ
Ⅱ![]() 若
若![]() ,直线
,直线![]() 与平面ABCM所成角的大小为
与平面ABCM所成角的大小为![]() ,求直线
,求直线![]() 与平面ABCM所成角的正弦值.
与平面ABCM所成角的正弦值.
【答案】(I)详见解析;(II)![]() .
.
【解析】
![]() Ⅰ
Ⅰ![]() 根据图形折叠前后的关系,先证明
根据图形折叠前后的关系,先证明![]() 面
面![]() ,利用线面垂直的性质可得出
,利用线面垂直的性质可得出![]() ;
;
![]() Ⅱ
Ⅱ![]() 由
由![]() Ⅰ
Ⅰ![]() 知,
知,![]() 面
面![]() ,所以平面
,所以平面![]() 面
面![]() ,过
,过![]() 作
作![]() ,则
,则![]() 平面
平面![]() ,
,![]() 是直线
是直线![]() 与平面
与平面![]() 所成角,可得
所成角,可得![]() 是等边三角形,
是等边三角形,![]() ,即
,即![]() ,从而可得
,从而可得![]() 是等腰三角形,
是等腰三角形,![]() 是直线
是直线![]() 与平面
与平面![]() 所成角在直角三角形
所成角在直角三角形![]() 中,利用直角三角形的性质求解即可.
中,利用直角三角形的性质求解即可.
![]() Ⅰ
Ⅰ![]() ,
,![]() ,
,![]() ,
,
![]() 面
面![]()
![]() 面
面![]() ,
,
![]() ;
;
![]() Ⅱ
Ⅱ![]() 由
由![]() Ⅰ
Ⅰ![]() 知,
知,![]() 面
面![]() ,
,![]() 平面ABCM,
平面ABCM,
![]() 平面
平面![]() 面
面![]() ,
,
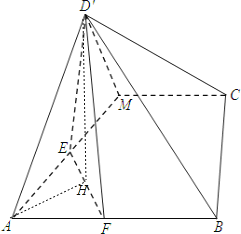
![]() 过
过![]() 作
作![]() ,则
,则![]() 平面ABCM,
平面ABCM,
![]() 也就是
也就是![]() 是直线
是直线![]() 与平面ABCM所成角,由已知,
与平面ABCM所成角,由已知,![]() ,
,
并且![]() 是所求的直线
是所求的直线![]() 与平面ABCM所成角.
与平面ABCM所成角.
![]() ,且
,且![]()
在三角形![]() 中,
中,![]() ,且
,且![]()
所以![]() 是等边三角形,
是等边三角形,![]() ,即
,即![]() ,
,![]() 是等腰三角形.
是等腰三角形.
设![]() ,
,![]() ,
,![]() ,四棱锥
,四棱锥![]() 的高
的高![]()
由于直线![]() 与平面ABCM所成角为
与平面ABCM所成角为![]() ,
,![]()

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目