题目内容
如图,直三棱柱 中,
中, ,
, 为
为 中点,求直线
中点,求直线 与平面
与平面 所成角的大小.(结果用反三角函数值表示)
所成角的大小.(结果用反三角函数值表示)
 .
.
解析试题分析:要求直线与平面所成的角,按照定义要作出直线在平面上的射影,直线与射影的夹角就是直线与平面所成的角,本题中平面 的垂线比较难以找到,但题中有
的垂线比较难以找到,但题中有 两两相互垂直,因此我们可以以他们为坐标轴建立空间直角坐标系,用向量法求出直线与平面所成的角.这样本题关键是求出平面
两两相互垂直,因此我们可以以他们为坐标轴建立空间直角坐标系,用向量法求出直线与平面所成的角.这样本题关键是求出平面 的法向量
的法向量 ,向量
,向量 与向量
与向量 的夹角与直线
的夹角与直线 与平面
与平面 所成的角互余.
所成的角互余.
试题解析:如图建立空间直角坐标系,设平面 的法向量
的法向量 ,
,
直线 与平面
与平面 所成角为
所成角为 :
:

 +2分
+2分
 +4分 令
+4分 令 ,则
,则 +6分
+6分
 +10分
+10分 
直线 与平面
与平面 所成角大小为
所成角大小为 +12分
+12分
考点:直线与平面所成的角.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中, 、
、 分别为
分别为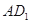 ,
, 中点。
中点。 与
与 所成角的大小;
所成角的大小; 平面
平面 。
。
 的底面边长为8的正方形,四条侧棱长均为
的底面边长为8的正方形,四条侧棱长均为 .点
.点 分别是棱
分别是棱 上共面的四点,平面
上共面的四点,平面 平面
平面 ,
, 平面
平面 .
.
 ,求四边形
,求四边形
 ,底面
,底面 为矩形,侧棱
为矩形,侧棱 ,其中
,其中 ,
, 为侧棱
为侧棱 上的两个三等分点,如下图所示.
上的两个三等分点,如下图所示. ;
; 与
与 所成角的余弦值;
所成角的余弦值; 的余弦值.
的余弦值.
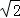 ,点E在侧棱AA1上,点F在侧棱BB1上,且AE=2
,点E在侧棱AA1上,点F在侧棱BB1上,且AE=2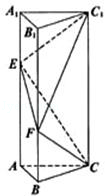
 的侧棱与底面垂直,且
的侧棱与底面垂直,且 ,
,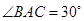 ,
, ,
, ,点
,点 、
、 、
、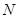 分别为
分别为 、
、 、
、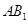 的中点.
的中点. 平面
平面 ;
; ;
; 的余弦值.
的余弦值.
 是边长为2的正方形,
是边长为2的正方形, 平面
平面 ,
, ,且
,且 .
.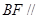 平面
平面 ;
; 平面
平面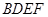 ;
; 的体积。
的体积。
 底面ABCD,侧棱
底面ABCD,侧棱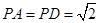 ,底面ABCD为直角梯形,其中BC//AD,AB
,底面ABCD为直角梯形,其中BC//AD,AB
 中,
中, ,
,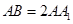 ,
, 是
是 的中点,△
的中点,△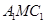 是等腰三角形,
是等腰三角形, 为
为 的中点,
的中点, 为
为 上一点.
上一点.
 ∥平面
∥平面 ;
;