题目内容
如图,在正方体 中,
中, 、
、 分别为
分别为 ,
, 中点。
中点。
(1)求异面直线 与
与 所成角的大小;
所成角的大小;
(2)求证: 平面
平面 。
。
(1) ;(2)见试题解析
;(2)见试题解析
解析试题分析:(1)把异面直线通过平移到一个平面内,即可求异面直线所成角。(2)由线面垂直的判定定理得,要证明 平面
平面 ,只需证明
,只需证明 垂直于平面
垂直于平面 内的两条相交直线,因为
内的两条相交直线,因为 ,
, ,
, 得
得 ,又
,又 平面
平面 ,且
,且 ,所以
,所以 平面
平面
试题解析:(1)解: 连结 。如图所示:
。如图所示:


 、
、 分别为
分别为 ,
, 中点。
中点。

 异面直线
异面直线 与
与 所成角即为
所成角即为 。(2分)
。(2分)
在等腰直角 中
中
故异面直线 与
与 所成角的大小为
所成角的大小为 。(4分)
。(4分)
(2)证明:在正方形中

 (6分)
(6分)
又
 平面
平面 (8分)
(8分)
考点:1、异面直线所成角的求法;2、线面垂直的判定

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
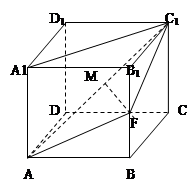
 中,
中, ,
, 分别是
分别是 的中点,且
的中点,且
 .
.
 与
与 所成角的大小;
所成角的大小; 与平面
与平面 所成角的正弦值.
所成角的正弦值.  的底面为菱形,
的底面为菱形,
 面
面 ,且
,且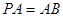 ,
,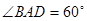 ,
,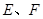 分别是
分别是 的中点.
的中点.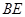 ∥平面
∥平面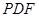 ;
;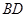 作一平面交棱
作一平面交棱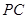 于点
于点 ,若二面角
,若二面角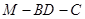 的大小为
的大小为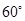 ,求
,求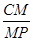 的值.
的值.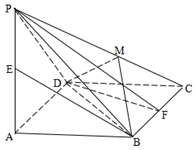
 中,
中,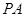 ⊥底面
⊥底面 ,四边形
,四边形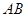 ⊥
⊥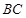 ,
,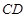 ,
,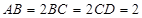 ,
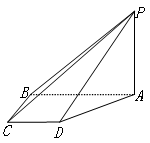
,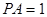 .
.
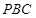 ⊥平面
⊥平面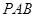 ;
;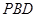 的距离;
的距离;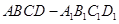 中,
中,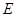 是
是 的中点.
的中点.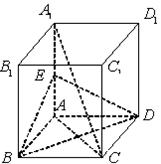
 平面
平面 ;
;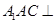 平面
平面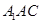 所成角的正弦值.
所成角的正弦值. 中,侧面
中,侧面 为菱形,
为菱形, 的中点为
的中点为 ,且
,且 平面
平面

 ,
, 求三棱柱
求三棱柱 中,
中, ,
, 为
为 中点,求直线
中点,求直线 与平面
与平面 所成角的大小.(结果用反三角函数值表示)
所成角的大小.(结果用反三角函数值表示)
 的大小是60°,线段
的大小是60°,线段 .
. ,
, 与
与 所成的角为30°.则
所成的角为30°.则 所成的角的正弦值是 .
所成的角的正弦值是 .