题目内容
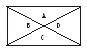
 17、如图,矩形的对角线把矩形分成A、B、C、D四部分,现用五种不同色彩给四部分涂色,每部分涂1种颜色,要求共边的两部分颜色互异,共有多少种不同的涂色方法?
17、如图,矩形的对角线把矩形分成A、B、C、D四部分,现用五种不同色彩给四部分涂色,每部分涂1种颜色,要求共边的两部分颜色互异,共有多少种不同的涂色方法?分析:由题意知给四部分涂色,至少要用两种颜色,故可分成三类涂色:第一类,用4种颜色涂色,第二类,用3种颜色涂色,第三类,用两种颜色涂色.分别写出三种不同情况下的结果,相加得到结果.
解答:解:由题意知给四部分涂色,至少要用两种颜色,故可分成三类涂色:
第一类,用4种颜色涂色,有A54种方法;
第二类,用3种颜色涂色,选3种颜色的方法有C53种;
在涂的过程中,选对顶的两部分(A、C或B、D)涂同色,
另两部分涂异色有C21种选法;3种颜色涂上去有A33种涂法.
共C53•C21•A33种涂法;
第三类,用两种颜色涂色.选颜色有C52种选法;
A、C与B、D各涂一色有A22种涂法.共C52•A22种涂法.
∴共有涂色方法A54+C53•C21•A33+C52•A22=260种.
第一类,用4种颜色涂色,有A54种方法;
第二类,用3种颜色涂色,选3种颜色的方法有C53种;
在涂的过程中,选对顶的两部分(A、C或B、D)涂同色,
另两部分涂异色有C21种选法;3种颜色涂上去有A33种涂法.
共C53•C21•A33种涂法;
第三类,用两种颜色涂色.选颜色有C52种选法;
A、C与B、D各涂一色有A22种涂法.共C52•A22种涂法.
∴共有涂色方法A54+C53•C21•A33+C52•A22=260种.
点评:本题可以这样解:区域A有5种涂色法;区域B有4种涂色法;区域C的涂色法有2类:若C与A涂同色,区域D有4种涂色法;若C与A涂不同色,此时区域C有3种涂色法,区域D也有3种涂色法.得到共有5×4×4+5×4×3×3=260种涂色法.

练习册系列答案
相关题目
 21、如图,已知矩形ABCD中,AB=10,BC=6,沿矩形的对角线BD把△ABD折起,使A移到A1点,且A1在平面BCD上的射影O恰好在CD上.
21、如图,已知矩形ABCD中,AB=10,BC=6,沿矩形的对角线BD把△ABD折起,使A移到A1点,且A1在平面BCD上的射影O恰好在CD上. 如图,矩形的对角线把矩形分成A、B、C、D四部分,现用五种不同色彩给四部分涂色,每部分涂1种颜色,要求共边的两部分颜色互异,共有( )种不同的涂色方法?
如图,矩形的对角线把矩形分成A、B、C、D四部分,现用五种不同色彩给四部分涂色,每部分涂1种颜色,要求共边的两部分颜色互异,共有( )种不同的涂色方法?