Question

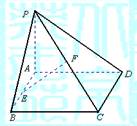
21、如图，已知矩形ABCD中，AB=10，BC=6，沿矩形的对角线BD把△ABD折起，使A移到A₁点，且A₁在平面BCD上的射影O恰好在CD上．
求证：（1）BC⊥A₁D；
（2）平面A₁BC⊥平面A₁BD．

Answer 1

分析：（1）通过证明BC⊥A₁O，BC⊥CO，证明BC⊥平面A₁CD，从而证明BC⊥A₁D，即由线线垂直推出线面垂直，再由线面垂直证出线线垂直．
（2）由（1）知BC⊥A₁D，因为ABCD为矩形，所以A₁B⊥A₁D，可证A₁D⊥平面A₁BC，从而达到目的，关键在一个平面内找到一条线和另一个平面垂直．

解答：证明：（1）由于A₁在平面BCD上的射影O在CD上，
则A₁O⊥平面BCD，又BC?平面BCD，
则BC⊥A₁O，
又BC⊥CO，A₁O∩CO=O，
则BC⊥平面A₁CD，又A₁D?平面A₁CD，
故BC⊥A₁D．
（2）因为ABCD为矩形，所以A₁B⊥A₁D，
由（1）知BC⊥A₁D，A₁B∩BC=B，则A₁D⊥平面A₁BC，又A₁D?平面A₁BD．
从而有平面A₁BC⊥平面A₁BD．

点评：本题考查线面垂直，面面垂直的判定，关键是正确进行线线垂直于面面垂直间的转化．