题目内容
在△ABC中,设角A,B,C的对边分别为a,b,c,且acosC+
c=b.
(1)求角A的大小;
(2)若a=
,b=4,求边c的大小.
| 1 |
| 2 |
(1)求角A的大小;
(2)若a=
| 15 |
考点:余弦定理,正弦定理
专题:三角函数的求值,解三角形
分析:(1)利用正弦定理化简已知等式,再利用内角和定理及诱导公式变形,根据sinC不为0求出cosA的值,即可确定出A的度数;
(2)由a,b,cosA的值,利用余弦定理求出c的值即可.
(2)由a,b,cosA的值,利用余弦定理求出c的值即可.
解答:
解:(1)利用正弦定理化简acosC+
c=b,得:sinAcosC+
sinC=sinB,
∵sinB=sin(A+C)=sinAcosC+cosAsinC,
∴sinAcosC+
sinC=sinAcosC+cosAsinC,即
sinC=cosAsinC,
∵sinC≠0,
∴cosA=
,
∵A为三角形内角,
∴A=
;
(2)∵a=
,b=4,cosA=
,
∴由余弦定理得:a2=b2+c2-2bccosA,15=16+c2-4c,即c2-4c+1=0,
解得:c=
=2±
.
| 1 |
| 2 |
| 1 |
| 2 |
∵sinB=sin(A+C)=sinAcosC+cosAsinC,
∴sinAcosC+
| 1 |
| 2 |
| 1 |
| 2 |
∵sinC≠0,
∴cosA=
| 1 |
| 2 |
∵A为三角形内角,
∴A=
| π |
| 3 |
(2)∵a=
| 15 |
| 1 |
| 2 |
∴由余弦定理得:a2=b2+c2-2bccosA,15=16+c2-4c,即c2-4c+1=0,
解得:c=
4±
| ||
| 2 |
| 3 |
点评:此题考查了正弦、余弦定理,两角和与差的正弦函数公式,熟练掌握定理是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在四棱锥A-BCDE中,底面四边形BCDE是等腰梯形,BC∥DE,∠DCB=45°,O是BC的中点,AO=
如图,在四棱锥A-BCDE中,底面四边形BCDE是等腰梯形,BC∥DE,∠DCB=45°,O是BC的中点,AO= 某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点.不包括右端点.如第一组表示收入在[1000,1500)
某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点.不包括右端点.如第一组表示收入在[1000,1500) 如图,斜三棱柱ABC-A1B1C1的侧棱长为
如图,斜三棱柱ABC-A1B1C1的侧棱长为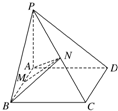 如图所示,已知PA⊥矩形ABCD所在平面,M,N分别是AB,PC的中点.
如图所示,已知PA⊥矩形ABCD所在平面,M,N分别是AB,PC的中点.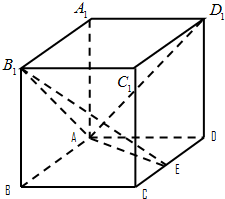 如图,在长方体ABCD-A1B1C1D1中AA1=AD=1,E为CD中点.
如图,在长方体ABCD-A1B1C1D1中AA1=AD=1,E为CD中点.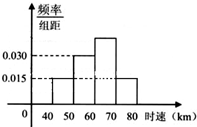 已知200辆汽车在通过某一段公路的时速的频率分布直方图如图所示,则时速在[60,70]之间的汽车大约有
已知200辆汽车在通过某一段公路的时速的频率分布直方图如图所示,则时速在[60,70]之间的汽车大约有