题目内容
已知函数f(x)=(a-
)x2+lnx(a∈R)
(1)当a=1时,求f(x)在区间[1,e]上的最大值和最小值;
(2)证明:当a∈(0,
]时,在区间(1,+∞)上,不等式f(x)<2ax恒成立.
| 1 |
| 2 |
(1)当a=1时,求f(x)在区间[1,e]上的最大值和最小值;
(2)证明:当a∈(0,
| 1 |
| 2 |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)当a=1时,f(x)=
x2+lnx,f′(x)=x+
=
,利用导数研究函数的单调性即可得出最值;
(2)令g(x)=f(x)-2ax=(a-
)x2-2ax+lnx,x∈(1,+∞),在区间(1,+∞)上,不等式f(x)<2ax恒成立?g(x)<0在区间(1,+∞)上恒成立.利用导数研究函数的单调性即可得出g(x)大值.
| 1 |
| 2 |
| 1 |
| x |
| x2+1 |
| x |
(2)令g(x)=f(x)-2ax=(a-
| 1 |
| 2 |
解答:
(1)解:当a=1时,f(x)=
x2+lnx,f′(x)=x+
=
,
对于x∈[1,e],有f'(x)>0,
∴f(x)在区间[1,e]上为增函数,
∴f(x)max=f(e)=1+
,f(x)min=f(1)=
.
(2)证明:令g(x)=f(x)-2ax=(a-
)x2-2ax+lnx,x∈(1,+∞),
在区间(1,+∞)上,不等式f(x)<2ax恒成立?g(x)max<0,x∈(1,+∞).
∵g′(x)=(2a-1)x-2a+
=
=
,
∴当a∈(0,
]时,则有2a-1≤0,此时在区间(1,+∞)上恒有g'(x)<0,
从而g(x)在区间(1,+∞)上是减函数;
∴g(x)<g(1),又g(1)=-a-
<0,
∴g(x)<0,即f(x)<2ax恒成立.
| 1 |
| 2 |
| 1 |
| x |
| x2+1 |
| x |
对于x∈[1,e],有f'(x)>0,
∴f(x)在区间[1,e]上为增函数,
∴f(x)max=f(e)=1+
| e2 |
| 2 |
| 1 |
| 2 |
(2)证明:令g(x)=f(x)-2ax=(a-
| 1 |
| 2 |
在区间(1,+∞)上,不等式f(x)<2ax恒成立?g(x)max<0,x∈(1,+∞).
∵g′(x)=(2a-1)x-2a+
| 1 |
| x |
| (2a-1)x2-2ax+1 |
| x |
| (x-1)[(2a-1)x-1] |
| x |
∴当a∈(0,
| 1 |
| 2 |
从而g(x)在区间(1,+∞)上是减函数;
∴g(x)<g(1),又g(1)=-a-
| 1 |
| 2 |
∴g(x)<0,即f(x)<2ax恒成立.
点评:本题考查了利用导数研究函数的单调性极值与最值、恒成立问题的等价转化方法,考查了构造函数法,考查了推理能力和计算能力,属于难题.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
已知i为虚数单位,则|
|=( )
| 1+i |
| i |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
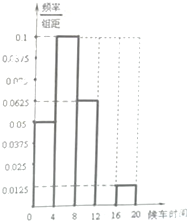 常州公交公司为了调整302线路发车的时间间隔,在某站点对乘客进行了候车时间的调查,以下是候车时间的频率分布表和频率分布直方图.
常州公交公司为了调整302线路发车的时间间隔,在某站点对乘客进行了候车时间的调查,以下是候车时间的频率分布表和频率分布直方图.