题目内容
10．
一个几何体的三视图如图所示，其中正视图和侧（左）视图是腰长为4的两个全等的等腰直角三角形，则该几何体的表面积为$32+16\sqrt{2}$．
分析 三视图对应的几何体是四棱锥，一条侧棱垂直底面，画出图形，根据三视图的数据，求出四棱锥的表面积．
解答 
解：几何体的直观图如图，底面边长为4，高为4，
所以四棱锥的表面积为：S=S底+2S侧+2S斜侧面=16+2×$\frac{1}{2}×4×4$+2×$\frac{1}{2}$×$4×4\sqrt{2}$=32+16$\sqrt{2}$．
故答案为：$32+16\sqrt{2}$．
点评 本题是基础题，考查三视图对应几何体的方法，四棱锥的表面积的求法，考查作图计算能力，常考题型．
练习册系列答案
相关题目
5．已知集合$M=\{x|x=m+\frac{1}{6}，m∈N\}$，$N=\{x|x=\frac{n}{2}-\frac{1}{3}，n∈N\}$，则M，N的关系为（ ）
| A． | M=N | B． | N?M | C． | M?N | D． | N⊆M |
15．已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=3x-1-m（m为常数），则f（log3$\frac{1}{5}$）=（ ）
| A． | 4 | B． | -4 | C． | $\frac{4}{5}$ | D． | -$\frac{4}{5}$ |
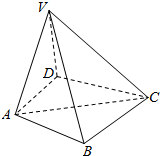如图，四棱锥V-ABCD中，∠BCD=∠BAD=90°，又∠BCV=∠BAV=90°求证：平面VDB⊥平面ABCD．
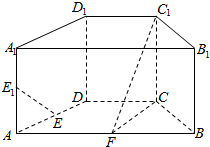如图，在直四棱柱ABCD-A1B1C1D1中，底面ABCD为等腰梯形，AB∥CD，AB=4，BC=CD=2，AA1=2，E、E1、F分别是棱AD、AA1、AB的中点．