题目内容
等差数列-21，-19，-17，…前
11
11
项和最小．分析：由题意可得an=2n-23，可得数列前11项为负，从第12项开始为正，进而可得答案．
解答：解：由题意可得等差数列的首项为-21，公差为-19-（-21）=2，
故其通项公式为：an=-21+2（n-1）=2n-23，
令2n-23≥0，解得n≥
，
故数列前11项为负，从第12项开始为正，
故数列的前11项和最小，
故答案为：11
故其通项公式为：an=-21+2（n-1）=2n-23，
令2n-23≥0，解得n≥
| 23 |
| 2 |
故数列前11项为负，从第12项开始为正，
故数列的前11项和最小，
故答案为：11
点评：本题考查等差数列的通项公式以及和的最值问题，属基础题．
练习册系列答案
相关题目
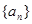，a2=9，a5=21
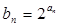,求数列｛bn｝的前n项和Sn。
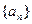，a2=9，a5=21
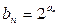,求数列｛bn｝的前n项和Sn。