题目内容
在平面直角坐标系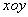 中,以原点
中,以原点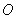 为圆心的圆
为圆心的圆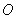 是曲线
是曲线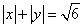 的内切圆.
的内切圆.
(1)求圆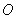 的方程;
的方程;
(2)若直线 与圆
与圆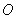 相切于第一象限,且与
相切于第一象限,且与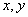 轴分别交于
轴分别交于 两点,当
两点,当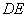 长最小时,求直线
长最小时,求直线 的方程;
的方程;
(3)设 是圆
是圆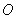 上任意两点,点
上任意两点,点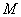 关于
关于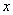 轴的对称点为
轴的对称点为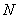 ,若直线
,若直线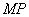 、
、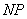 分别交于
分别交于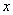 轴于点
轴于点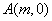 和
和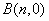 ,问这两点的横坐标之积
,问这两点的横坐标之积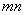 是否为定值?若是,请求出该定值;若不是,请说明理由.
是否为定值?若是,请求出该定值;若不是,请说明理由.
1)当 ,
, 时,曲线
时,曲线 是以点
是以点 ,
, 为端点的线段,
为端点的线段,
根据对称性可知,曲线是由 ,
, ,
,  ,
, 围成的正方形,
围成的正方形,
 圆O的半径
圆O的半径 ,
, 圆O的方程为
圆O的方程为 .
.

令 ,
,

 即
即 时,
时, 最大,此时
最大,此时 最大,
最大, ,
,
 直线
直线 :
: .
.
(3)设 ,
, ,则
,则 ,
, ,
, ,
,
 直线
直线 的方程:
的方程: ,令
,令 ,
,
解得 ,同理
,同理 ,
,

 .
.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 中,
中, 与平面
与平面 所成角的余弦值为
所成角的余弦值为  中,有命题
中,有命题 ;②
;② ;③若
;③若 ,则
,则 ,则
,则 个 B.
个 B.  个 C.
个 C.  个 D.
个 D.  个
个 ,则
,则
 ,3) D.(5,9)
,3) D.(5,9) 交于M、N两点,且M、N关于直线
交于M、N两点,且M、N关于直线 对称,则直线l被圆截得的弦长为( )
对称,则直线l被圆截得的弦长为( )
 为等差数列,且
为等差数列,且 ( )
( ) B、
B、 C、
C、 D、2
D、2 的解集是
的解集是 } B、{
} B、{ }
} } D、{
} D、{ }
}