题目内容
已知向量a=3e1-2e2,b=4e1+e2,其中e1=(1,0),e2=(0,1),求:
(1)a·b,|a+b|;(2)a与b的夹角的余弦值.
解:(1)a=3(1,0)-2(0,1)=(3,-2),
b=4(1,0)+(0,1)=(4,1),
a·b=3×4+(-2)×1=10 ∵|a+b|2=(a+b)2=a2+2a·b+b2
=|a|2+20+|b|2=13+20+17=50,
∴|a+b|=5
(2)cos〈a,b〉=

练习册系列答案
相关题目

 且
且 ,那么下列不等式中不一定成立的是( )
,那么下列不等式中不一定成立的是( ) B.
B. C.
C. D.
D.
 ,
, ,则边长
,则边长 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
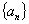 的前
的前 项和为
项和为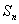 ,对任意的正整数
,对任意的正整数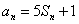 成立,记
成立,记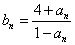 .(1)求数列
.(1)求数列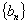 的通项公式;
的通项公式;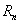 ,是否存在正整数
,是否存在正整数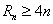 成立?若存在,找出一个正整数
成立?若存在,找出一个正整数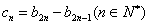 ,设数列
,设数列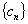 的前
的前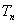 ,求证:对于
,求证:对于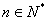 都有
都有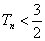
 在
在 处的切线为
处的切线为 B、
B、
 D、
D、
 的最小正周期为
的最小正周期为  B.
B. C.
C. D.
D.
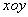 中,以原点
中,以原点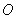 为圆心的圆
为圆心的圆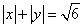 的内切圆.
的内切圆. 与圆
与圆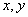 轴分别交于
轴分别交于 两点,当
两点,当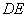 长最小时,求直线
长最小时,求直线 是圆
是圆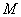 关于
关于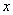 轴的对称点为
轴的对称点为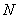 ,若直线
,若直线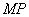 、
、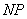 分别交于
分别交于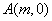 和
和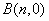 ,问这两点的横坐标之积
,问这两点的横坐标之积 是否为定值?若是,请求出该定值;若不是,请说明理由.
是否为定值?若是,请求出该定值;若不是,请说明理由.