题目内容
3.在数列{an}中,a1=1,且${a_{n+1}}=\frac{a_n}{{1+{a_n}}}$,n∈N*,①求a2,a3,a4并猜想数列的通项公式,②试证明你的猜想.分析 ①利用数列的递推关系式求出数列的前4项,然后猜想数列的通项公式.
②利用递推关系式判断新数列$\{\frac{1}{{a}_{n}}\}$是以1为首项,公差d=1的等差数列,利用等差数列的通项公式求解即可.
解答 解:①∵a1=1,且${a_{n+1}}=\frac{a_n}{{1+{a_n}}}$,n∈N*,∴${a}_{2}=\frac{{a}_{1}}{1+{a}_{1}}$=$\frac{1}{2}$;${a}_{3}=\frac{{a}_{2}}{1+{a}_{2}}$=$\frac{1}{3}$,同理
得:${a}_{4}=\frac{{a}_{3}}{1+{a}_{3}}=\frac{1}{4}$,观察可得,数列的前4项都等于相应序号的倒数,
由此猜想:${a}_{n}=\frac{1}{n}$,n∈N*,------(6分)
②证明如下:∵${a_{n+1}}=\frac{a_n}{{1+{a_n}}}$,∴$\frac{1}{{a}_{n+1}}=\frac{1+{a}_{n}}{{a}_{n}}$=$\frac{1}{{a}_{n}}+1$,
∴$\frac{1}{{a}_{n+1}}-\frac{1}{{a}_{n}}=1$,∈N*,
∴$\{\frac{1}{{a}_{n}}\}$是以$\frac{1}{{a}_{1}}=1$为首项,公差d=1的等差数列,
∴$\frac{1}{{a}_{n}}$=1+(n-1)×1=n,∴an=$\frac{1}{n}$,∈N*.------(12分)
点评 本题考查数列的递推关系式的应用,数列的通项公式的求法,考查转化思想与计算能力.

练习册系列答案
相关题目
13.已知α是第三象限角且$|{cos\frac{α}{3}}|=-cos\frac{α}{3}$,则$\frac{α}{3}$角是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
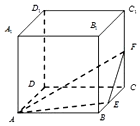 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E,F分别是棱BC,CC1的中点,P是侧面BCC1B1内一点,若A1P∥平面AEF,则线段AP长度的取值范围是[$\frac{3\sqrt{2}}{4}$,$\frac{\sqrt{5}}{2}$].
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E,F分别是棱BC,CC1的中点,P是侧面BCC1B1内一点,若A1P∥平面AEF,则线段AP长度的取值范围是[$\frac{3\sqrt{2}}{4}$,$\frac{\sqrt{5}}{2}$].