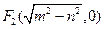题目内容
已知双曲线 的两个焦点为
的两个焦点为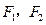 ,实半轴长与虚半轴长的乘积为
,实半轴长与虚半轴长的乘积为 .直线
.直线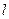 过
过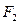 点且与线段
点且与线段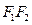 的夹角为
的夹角为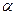 且
且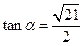 ,
,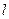 与线段
与线段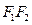 垂直平分线的交点为
垂直平分线的交点为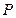 ,线段
,线段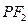 与双曲线的交点为
与双曲线的交点为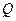 ,且
,且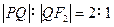 ,求双曲线方程.
,求双曲线方程.
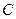 的两个焦点为
的两个焦点为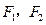 ,实半轴长与虚半轴长的乘积为
,实半轴长与虚半轴长的乘积为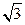 .直线
.直线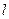 过
过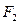 点且与线段
点且与线段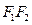 的夹角为
的夹角为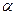 且
且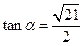 ,
,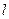 与线段
与线段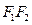 垂直平分线的交点为
垂直平分线的交点为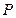 ,线段
,线段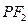 与双曲线的交点为
与双曲线的交点为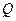 ,且
,且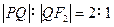 ,求双曲线方程.
,求双曲线方程. 或
或
从双曲线的对称性知,我们可以取以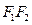 所在直线为
所在直线为 轴,过
轴,过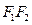 中点且垂直于
中点且垂直于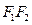 的直线为
的直线为 轴建立直角坐标系如图所示,
轴建立直角坐标系如图所示,
设双曲线方程为 ,用待定系数法求
,用待定系数法求 之值,又设
之值,又设 ,
, .
.
从题设知道直线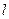 方程为
方程为 ,
,
即 ,在方程中令
,在方程中令 ,得点
,得点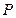 坐标
坐标 .
. ,
,
由定比分点坐标公式可得点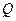 坐标为
坐标为 .
.
 点
点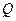 在双曲线上,
在双曲线上, . ①
. ①
又 , ② 从题设有
, ② 从题设有 , ③
, ③
从式①,②消去 ,化简整理得
,化简整理得 .
.
解此方程得 ,或
,或 (舍去).
(舍去).
 ,
, ,
, . ④
. ④
由③,④得 ,
, .
.
故所求双曲线方程为 ,从对称性知,双曲线
,从对称性知,双曲线 也适合.
也适合.
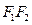 所在直线为
所在直线为 轴,过
轴,过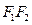 中点且垂直于
中点且垂直于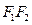 的直线为
的直线为 轴建立直角坐标系如图所示,
轴建立直角坐标系如图所示,设双曲线方程为
 ,用待定系数法求
,用待定系数法求 之值,又设
之值,又设 ,
, .
.从题设知道直线
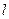 方程为
方程为 ,
,即
 ,在方程中令
,在方程中令 ,得点
,得点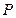 坐标
坐标 .
. ,
,由定比分点坐标公式可得点
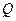 坐标为
坐标为 .
. 点
点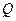 在双曲线上,
在双曲线上, . ①
. ①又
 , ② 从题设有
, ② 从题设有 , ③
, ③从式①,②消去
 ,化简整理得
,化简整理得 .
.解此方程得
 ,或
,或 (舍去).
(舍去). ,
, ,
, . ④
. ④由③,④得
 ,
, .
.故所求双曲线方程为
 ,从对称性知,双曲线
,从对称性知,双曲线 也适合.
也适合.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
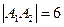 ,焦距
,焦距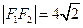 ,过焦点
,过焦点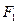 作一直线,交椭圆于
作一直线,交椭圆于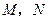 两点.设
两点.设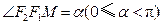 ,当
,当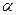 取何值时,
取何值时,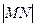 等于椭圆短轴的长?
等于椭圆短轴的长?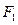 ,
,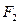 为椭圆
为椭圆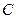 :
: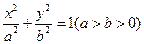 的左、右两个焦点,直线
的左、右两个焦点,直线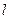 :
: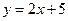 与椭圆
与椭圆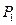 ,
,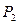 ,已知椭圆中心
,已知椭圆中心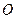 点关于
点关于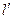 上.
上.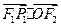 ,
,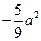 ,
,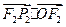 成等差数列,求椭圆
成等差数列,求椭圆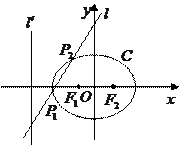
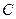 的中心在原点
的中心在原点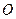 ,焦点在
,焦点在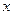 轴上,右准线的方程为
轴上,右准线的方程为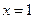 ,倾斜角为
,倾斜角为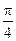 的直线
的直线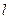 交椭圆
交椭圆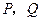 两点,且
两点,且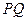 的中点坐标为
的中点坐标为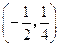 ,设
,设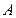 为椭圆
为椭圆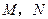 为椭圆
为椭圆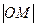 ,
,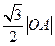 ,
,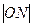 三者的平方成等差数列,则直线
三者的平方成等差数列,则直线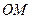 和
和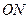 斜率之积的绝对值是否为定值,若是,请求出定值;若不是,请说明理由.
斜率之积的绝对值是否为定值,若是,请求出定值;若不是,请说明理由.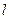 交椭圆
交椭圆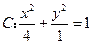 于
于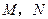 两点,且
两点,且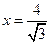 的距离之和为
的距离之和为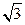 ,求直线
,求直线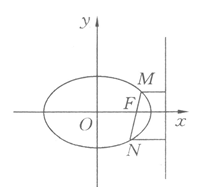

 到直线
到直线 的距离与它到点
的距离与它到点 的距离之比为
的距离之比为 ,求动点
,求动点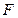 的坐标为
的坐标为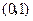 ,直线
,直线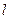 的方程为
的方程为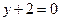 ,动点
,动点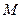 到点
到点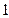 ,求动点
,求动点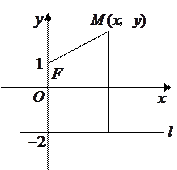
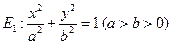 的一条弦,M(2,1)是AB的中点,以M为焦点且以椭圆E1的右准线为相应准线的双曲线E2与直线AB交于点
的一条弦,M(2,1)是AB的中点,以M为焦点且以椭圆E1的右准线为相应准线的双曲线E2与直线AB交于点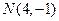 . (1)设双曲线E2的离心率为
. (1)设双曲线E2的离心率为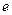 ,求
,求 的函数表达式; (2)当椭圆E1与双曲线E2的离心率互为倒数时,求椭圆E1的方程.
的函数表达式; (2)当椭圆E1与双曲线E2的离心率互为倒数时,求椭圆E1的方程.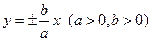 的双曲线的标准方程一定是
的双曲线的标准方程一定是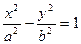
 的准线方程是
的准线方程是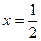
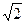
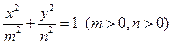 的焦点坐标是
的焦点坐标是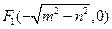 ,
,