题目内容
(12分)已知AB是椭圆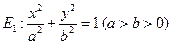 的一条弦,M(2,1)是AB的中点,以M为焦点且以椭圆E1的右准线为相应准线的双曲线E2与直线AB交于点
的一条弦,M(2,1)是AB的中点,以M为焦点且以椭圆E1的右准线为相应准线的双曲线E2与直线AB交于点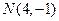 . (1)设双曲线E2的离心率为
. (1)设双曲线E2的离心率为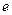 ,求
,求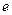 关于
关于 的函数表达式; (2)当椭圆E1与双曲线E2的离心率互为倒数时,求椭圆E1的方程.
的函数表达式; (2)当椭圆E1与双曲线E2的离心率互为倒数时,求椭圆E1的方程.
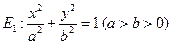 的一条弦,M(2,1)是AB的中点,以M为焦点且以椭圆E1的右准线为相应准线的双曲线E2与直线AB交于点
的一条弦,M(2,1)是AB的中点,以M为焦点且以椭圆E1的右准线为相应准线的双曲线E2与直线AB交于点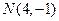 . (1)设双曲线E2的离心率为
. (1)设双曲线E2的离心率为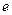 ,求
,求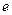 关于
关于 的函数表达式; (2)当椭圆E1与双曲线E2的离心率互为倒数时,求椭圆E1的方程.
的函数表达式; (2)当椭圆E1与双曲线E2的离心率互为倒数时,求椭圆E1的方程.(1)  (2)
(2) 
 (2)
(2) 
(1)椭圆的右准线: .
.  即
即
又AB方程: ,
,
 ,
,
 ,∴
,∴ 即
即
∴椭圆的离心率 .从而
.从而
(2)由题设 即
即 .∴
.∴ . 解之:
. 解之: 或
或 .若
.若 时,由M(2,1)在椭圆内,矛盾.∴
时,由M(2,1)在椭圆内,矛盾.∴ .从而椭圆方程为:
.从而椭圆方程为: 为所求.
为所求.
 .
.  即
即
又AB方程:
 ,
, ,
,
 ,∴
,∴ 即
即
∴椭圆的离心率
 .从而
.从而
(2)由题设
 即
即 .∴
.∴ . 解之:
. 解之: 或
或 .若
.若 时,由M(2,1)在椭圆内,矛盾.∴
时,由M(2,1)在椭圆内,矛盾.∴ .从而椭圆方程为:
.从而椭圆方程为: 为所求.
为所求.
练习册系列答案
相关题目
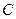 的两个焦点为
的两个焦点为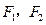 ,实半轴长与虚半轴长的乘积为
,实半轴长与虚半轴长的乘积为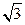 .直线
.直线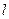 过
过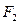 点且与线段
点且与线段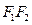 的夹角为
的夹角为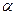 且
且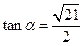 ,
,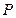 ,线段
,线段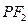 与双曲线的交点为
与双曲线的交点为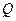 ,且
,且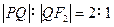 ,求双曲线方程.
,求双曲线方程.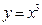 在
在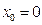 处的切线是否存在,若存在,求出切线的斜率和切线方程;若不存在,请说明理由.
处的切线是否存在,若存在,求出切线的斜率和切线方程;若不存在,请说明理由.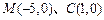 ,
,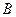 分
分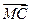 所成的比为2,
所成的比为2,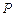 是平面上一动点,且满足
是平面上一动点,且满足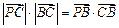 .(1)求点
.(1)求点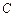 对应的方程;(2) 已知点
对应的方程;(2) 已知点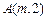 在曲线
在曲线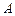 作曲线
作曲线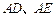 ,且直线
,且直线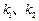 满足
满足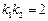 ,试推断:动直线
,试推断:动直线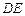 有何变化规律,证明你的结论.
有何变化规律,证明你的结论. )、N(-4,-
)、N(-4,-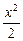 +y2="1," ④
+y2="1," ④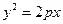 的焦点与双曲线
的焦点与双曲线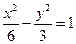 的右焦点重合,则
的右焦点重合,则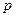 的值为 .
的值为 .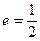
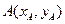 和
和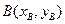 两点分别在射线
两点分别在射线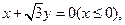
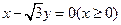 上移动,且
上移动,且 ,动点P满足
,动点P满足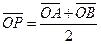 ,
,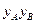 的值;
的值; 与曲线C交于M、N两点,且M、N两点都在以G为圆心的圆上,求
与曲线C交于M、N两点,且M、N两点都在以G为圆心的圆上,求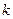 的取值范围.
的取值范围.