题目内容
双曲线
上一点P的两条焦半径夹角为60°，F1，F2为焦点，则△PF1F2的面积为 ．
【答案】分析：由双曲线的性质知|PF1|2+|PF2|2-2|PF1||PF2|=100…（1），由余弦定理可知|PF1|2+|PF2|2-2|PF1||PF2|cos60°=164…（2），由（1）、（2）联立方程组，解得|PF1||PF2|=64，由此可以求出△PF1F2的面积．
解答：解：∵|PF1|-|PF2|=10，∴|PF1|2+|PF2|2-2|PF1||PF2|=100…（1）
∵双曲线
上一点P的两条焦半径夹角为60°，
∴由余弦定理可知|PF1|2+|PF2|2-2|PF1||PF2|cos60°=164…（2），
由（1）、（2）联立方程组，解得|PF1||PF2|=64，
∴△PF1F2的面积=
=16
．
答案：16
．
点评：利用余弦定理解决圆锥曲线问题是求解高考题的常规方法．
解答：解：∵|PF1|-|PF2|=10，∴|PF1|2+|PF2|2-2|PF1||PF2|=100…（1）
∵双曲线
上一点P的两条焦半径夹角为60°，∴由余弦定理可知|PF1|2+|PF2|2-2|PF1||PF2|cos60°=164…（2），
由（1）、（2）联立方程组，解得|PF1||PF2|=64，
∴△PF1F2的面积=
=16．答案：16
．点评：利用余弦定理解决圆锥曲线问题是求解高考题的常规方法．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
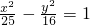上一点P的两条焦半径夹角为60°，F1，F2为焦点，则△PF1F2的面积为________．
=1（b＞0）的左、右焦点，过F2作垂直于x轴的直线，在x轴上方交双曲线于点M，且∠MF1F2=30°，圆O的方程为x2+y2=b2．
的值．