题目内容
设虚数z满足|2z+15|=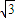 |
|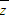 +10|.
+10|.(1)计算|z|的值;
(2)是否存在实数a,使
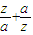 ∈R?若存在,求出a的值;若不存在,说明理由.
∈R?若存在,求出a的值;若不存在,说明理由.
【答案】分析:(1)设z=a+bi(a,b∈R且b≠0)则 代入条件|2z+15|=
代入条件|2z+15|= |
| +10|然后根据复数的运算法则和模的概念将上式化简可得
+10|然后根据复数的运算法则和模的概念将上式化简可得 即求出了|z|的值
即求出了|z|的值
(2)对于此种题型可假设存在实数a使 ∈R根据复数的运算法则设(z=c+bi(c,b∈R且b≠0))可得
∈R根据复数的运算法则设(z=c+bi(c,b∈R且b≠0))可得 =
= +(
+( )∈R即
)∈R即 =0再结合b≠0和(1)的结论即可求解.
=0再结合b≠0和(1)的结论即可求解.
解答:解:(1)设z=a+bi(a,b∈R且b≠0)则
∵|2z+15|= |
| +10|
+10|
∴|(2a+15)+2bi|= |(a+10)-bi|
|(a+10)-bi|
∴ =
=
∴a2+b2=75
∴
∴|z|=
(2)设z=c+bi(c,b∈R且b≠0)假设存在实数a使 ∈R
∈R
则有 =
= +(
+( )∈R
)∈R
∴ =0
=0
∵b≠0
∴a=

由(1)知 =5
=5
∴a=±5
点评:本题主要考查了求解复数的模.解题的关键是要熟记复数模的概念:z=a+bi(a,b∈R)则|z|= !
!
 代入条件|2z+15|=
代入条件|2z+15|= |
| +10|然后根据复数的运算法则和模的概念将上式化简可得
+10|然后根据复数的运算法则和模的概念将上式化简可得 即求出了|z|的值
即求出了|z|的值(2)对于此种题型可假设存在实数a使
 ∈R根据复数的运算法则设(z=c+bi(c,b∈R且b≠0))可得
∈R根据复数的运算法则设(z=c+bi(c,b∈R且b≠0))可得 =
= +(
+( )∈R即
)∈R即 =0再结合b≠0和(1)的结论即可求解.
=0再结合b≠0和(1)的结论即可求解.解答:解:(1)设z=a+bi(a,b∈R且b≠0)则

∵|2z+15|=
 |
| +10|
+10|∴|(2a+15)+2bi|=
 |(a+10)-bi|
|(a+10)-bi|∴
 =
=
∴a2+b2=75
∴

∴|z|=

(2)设z=c+bi(c,b∈R且b≠0)假设存在实数a使
 ∈R
∈R则有
 =
= +(
+( )∈R
)∈R∴
 =0
=0∵b≠0
∴a=


由(1)知
 =5
=5
∴a=±5

点评:本题主要考查了求解复数的模.解题的关键是要熟记复数模的概念:z=a+bi(a,b∈R)则|z|=
 !
! 
练习册系列答案
相关题目