题目内容
已知E、F、G、H分别是空间四边形ABCD各边AB、AD、CB、CD上的点,且直线EF和HG交于点P.?求证:B、D、P在同一直线上.(用三段论证)?
思路分析:用三段论证明,大前提应是如果三个点都在两个平面的交线上,那么这三个点共线.??
证明:∵平面ABD和平面BCD的交线BD上的任意三个点共线,(大前提)?
又∵P∈EF,P∈GH,?
∴P∈平面ABD,P∈平面BCD.?
∴P∈BD=平面ABD∩平面CBD.?
又B、D∈BD,
∴B、P、D∈BD.(小前提)?
∴B、D、P在同一直线上.(结论).
练习册系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
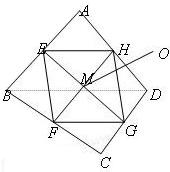已知E，F，G，H分别是空间四边形ABCD的边AB，BC，CD，DA的中点．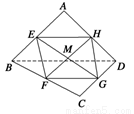
=
（
+
+
+
）.
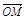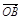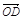